What Does The 3 Mean In Math
In mathematics, the expression 3! is read as three factorial and is really a shorthand way to denote the multiplication of several consecutive whole numbers. Since there are many places throughout mathematics and statistics where we need to multiply numbers together, the factorial is quite useful.
Three Major Components Of Effective Schema Instruction
Effective schema instruction incorporates the principles of explicit instruction, which have been shown to be necessary for students with learning disabilities . This includes providing explanations in simple, direct language modeling efficient solution strategies instead of expecting students to discover strategies on their own ensuring students have the necessary background knowledge and skills to succeed with those strategies gradually fading support providing multiple practice opportunities and incorporating systematic cumulative review. As with attack strategies, the number of practice opportunities differs within schema instruction depending on the students incoming knowledge and skills, as well as the quality of teacher modeling, explanations, and corrective feedback.
The Difference Between All Together And Altogether
All together refers to all the members of a group. It can mean everyone or everything together, or simply in a group:
Its not uncommon to see a noun or a verb between the elements of the phrase:
Heres a tip:
Altogether is altogether different from all together. Its not a phraseits a single-word adverb that means completely,all things considered, on the whole, or all in all:
Read Also: Beth Thomas Story
What Do Some Words Mean To Add In Math
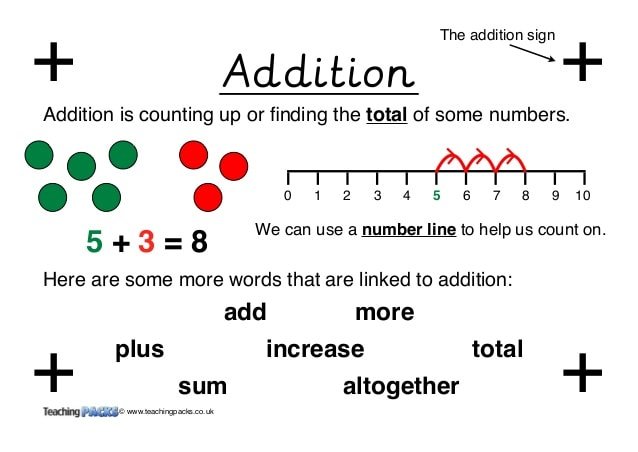
Add an observation that is bigger than the mean or remove an observation that is smaller than the mean. What are some words that mean to add in math? more, plus, deposit, add, gain, raise, increase, sum, total What does length mean in math? What does length mean in math What does comparison mean in math? in math
What Is The Significance Of Game Theory

CONCLUSION. Game theory is a classic theory which applicable all most all the field. The main significant of game theory is to formulate the alternative strategy to compete with one another and in the same sense it is an essential tool for decision making process according to fluctuations in relevant contents.
You May Like: Kuta Software Infinite Geometry Volume Of Prisms And Cylinders
Princeton’s Wordnetrate This Definition:
raw, altogether, birthday suitadverb
“in the raw” “in the altogether” “in his birthday suit”
wholly, entirely, completely, totally, all, altogether, wholeadverb
to a complete degree or to the full or entire extent
“he was wholly convinced” “entirely satisfied with the meal” “it was completely different from what we expected” “was completely at fault” “a totally new situation” “the directions were all wrong” “it was not altogether her fault” “an altogether new approach” “a whole new idea”
altogether, all told, in alladverb
with everything included or counted
“altogether he earns close to a million dollars”
all in all, on the whole, altogether, tout ensembleadverb
with everything considered
“altogether, I’m sorry it happened” “all in all, it’s not so bad”
Teaching Word Problem Structures
As when teaching any strategy, teachers should use explicit, systematic instruction when introducing schema instruction, sometimes referred to as schema-based instruction . Although the same process is used to teach any schema, for illustrative purposes, the steps for how to teach the combine schema are outlined in the box below.
| Step1: Teach students to identify different problem types and practice translating the information into a diagram or equation. |
| Descriptions |
Don’t Miss: Fsa Algebra 1 Eoc Practice Test Answers
Teach Important Vocabulary And Language Constructions
Word-problem solving relies heavily on reading and understanding language. Typically developing students often understand important math vocabulary prior to school entry and gradually learn to treat this language in a special, task-specific way involving more complicated constructions about sets . Many teachers assume that students have the necessary language comprehension to understand word problems and the problems schema. But for students with learning disabilities, this is a shaky assumption.
A strong focus on vocabulary and language is therefore important, especially for students with learning disabilities. Examples of vocabulary and constructions that require explicit instruction, focused on the meaning of the language, are joining words and superordinate categories in combine problems compare words and adjective –er versus verb –er words in compare problems and cause-effect conjunctions , implicit change verbs , and time passage phrases in change problems. We also recommend a focus on confusing cross-problem constructions and tricky labels .
What Is The Not Equal To Sign In Matlab
This page contains a comprehensive listing of all MATLAB® operators, symbols, and special characters.Relational Operators.
| Symbol |
|---|
- clear allclear all variables in your workspace.
- plotPlot curves by inserting vectors of the same length in the function.
- subplotPlot multiple figures in one window.
- axisSet the minimum x and y axis of your plot.
- legendName the data series of your figure.
Read Also: Does Elton John Have Biological Children
Summing Up: What To Do
Schema instruction can be a powerful tool for helping students understand and solve word problems. Schema instruction facilitates mathematical reasoning by helping students understand the underlying structures within word problems that will be used across grade levels and with whole and rational numbers. To close, we summarize several key dos and do nots for teaching schemas.
Do not teach students to solve word problems by isolating key words and linking those words to operations. Dont say things like tells us to divide. Teaching students what means helps students understand the conceptual schema of the word problem but telling students to divide whenever they see is error fraught. In a similar vein, do not define word problems by an operation. Do not say, Today were working on division word problems. There is no such thing as a subtraction word problem because some students may use addition to solve such a problem others may use subtraction. Defining a word problem by operation undermines conceptual understanding.
Does How Many Mean Subtract
Subtraction, Subtract, Minus, Less, Difference, Decrease, Take Away, Deduct. × Multiplication, Multiply, Product, By, Times, Lots Of. ÷ Division, Divide, Quotient, Goes Into, How Many Times.
How many more is add or subtract?
Addition-sum, altogether, all, in all, together, total, total number, add, increase, increased by, more than. Subtraction-minus, greater than, take away, fewer than, less than, subtract, decreased by. Multiplication-product, multiply, multiplied by, times.
You May Like: Geometry Segment Addition Postulate Worksheet
Does Fewer Mean Add Or Subtract
AdditionaddSubtractiontake awayfewerlesssubtract
Yes, usually, “fewer” means subtraction, but some questions might try to trick you!
Furthermore, what does the word fewer mean in math? fewer trains were late Synonyms: few. a quantifier that can be used with count nouns and is often preceded by `a’ a small but indefinite number. less. a quantifier meaning not as great in amount or degree.
Similarly one may ask, does how many mean subtract?
Subtraction, Subtract, Minus, Less, Difference, Decrease, Take Away, Deduct. × Multiplication, Multiply, Product, By, Times, Lots Of. ÷ Division, Divide, Quotient, Goes Into, How Many Times.
How many more is add or subtract?
Addition-sum, altogether, all, in all, together, total, total number, add, increase, increased by, more than. Subtraction-minus, greater than, take away, fewer than, less than, subtract, decreased by. Multiplication-product, multiply, multiplied by, times.
Why Is Calculus So Hard
So be proud of yourself, and realize that you are not alone. Mot people find calculus very hard. One of the reasons why calculus is so difficult arises from a lack of understanding about the nature of the subject. … The solution of many problems will involve trigonometry, geometry and algebra and calculus.
Don’t Miss: Who Are Paris Jackson’s Biological Parents
A Note On Equal Precedence
Since multiplication and division are of equal precedence, it may be helpful to think of dividing by a number as multiplying by the reciprocal of that number. Thus 3 \div 4 = 3 \cdot \frac. In other words, the quotient of 3 and 4 equals the product of 3 and \frac.
Similarly, as addition and subtraction are of equal precedence, we can think of subtracting a number as the same as adding the negative of that number. Thus 34=3+. In other words, the difference of 3 and 4 equals the sum of positive three and negative four.
With this understanding, think of 13+7 as the sum of 1, negative 3, and 7, and then add these terms together. Now that youve reframed the operations, any order will work:
- +7=2+7=5
- +1=4+1=5
The important thing is to keep the negative sign with any negative number .
Rules Of Ordering In Mathematics
BODMAS is a useful acronym that tells you the order in which you solve mathematical problems. It’s important that you follow the rules of BODMAS, because without it your answers can be wrong.
The BODMAS acronym is for:
- Brackets .
- Orders .
- Division.
The Skills You Need Guide to Numeracy
This four-part guide takes you through the basics of numeracy from arithmetic to algebra, with stops in between at fractions, decimals, geometry and statistics.
Whether you want to brush up on your basics, or help your children with their learning, this is the book for you.
Read Also: What Are The Three Types Of Research Methods In Psychology
Does Magnitude Have Direction
A quantity which does not depend on direction is called a scalar quantity. Vector quantities have two characteristics, a magnitude and a direction. Scalar quantities have only a magnitude. When comparing two vector quantities of the same type, you have to compare both the magnitude and the direction.
Teaching A Solution Strategy For Each Schema
After students understand the meaning of a schema , students learn to select a solution strategy and use the solution strategy to organize the information from the word problem. Teaching a solution strategy involves modeling from the teacher and practice opportunities in which students receive feedback from the teacher.
Now that Mrs. Franks students understand what the compare schema means and have mastered the RUN attack strategy within combine schema instruction, Mrs. Frank explicitly models how to solve compare problems. Initially, she uses a word problem with a difference missing. Students complete the same set of activities with the graphic organizer and equation, writing missing information into the graphic organizer and using a blank or question mark to represent the missing information in the equation. Gradually, Mrs. Frank omits the concrete manipulatives, integrates novel names into problems, and substitutes a hand gesture for easy reference to the graphic organizer .
After students learn to recognize word problems as belonging to schemas and are consistently using an efficient solution strategy to organize the necessary word-problem information, the next phase of instruction involves explicitly teaching word-problem specific vocabulary and language.
Don’t Miss: What Is An Example Of Movement In Geography
Additive And Multiplicative Schemas
Schema instruction is a demonstrably effective instructional practice for promoting stronger word-problem performance for students with learning disabilities across grade levels . Whereas defining word problems by key words or operation has no research to support use for students with learning disabilities, schema instruction has a rich research base. Two categories of schemas that have broad usage for teachers are the additive and multiplicative schemas. These schemas can be used to solve word problems from kindergarten through eighth grade.
Difficulty With Word Problems
Most students, especially those with mathematics difficulties and disabilities, have trouble solving word problems. This is in large part because word problems require students to:
Students who experience difficulty with any of the steps listed above, such as students who struggle with mathematics, will likely arrive at an incorrect answer.
Recommended Reading: Elton John Wife And Kids
What Does And Mean In Math Terms
meansmathematicsmathematicsmean
jamie says: It means greater than you could reverse the mathequation to 12 < 5x-9 and it would be read as “less than”. An easy way to remember is to think of the symbol as an alligator’s mouth the alligator always wants to eat the bigger thing! Reply.
Beside above, what is a term in mathematics? In Algebra a term is either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or signs, or sometimes by divide.
Herein, does and mean multiply?
In probability, the words “AND” and “OR” are kind of special, and they usually mean multiply the probabilities and add the probabilities , respectively. –
Does and mean add or subtract?
Addition-sum, altogether, all, in all, together, total, total number, add, increase, increased by, more than. Subtraction-minus, greater than, take away, fewer than, less than, subtract, decreased by. Multiplication-product, multiply, multiplied by, times.
Examples Of Altogether In A Sentence

altogetheraltogetheraltogetherAltogetheraltogetheraltogether Los Angeles TimesaltogetherBostonGlobe.comaltogetherABC NewsaltogetherCNNaltogether Washington PostaltogetherRolling Stonealtogether BGRaltogetherFox Newsaltogether WSJ
These example sentences are selected automatically from various online news sources to reflect current usage of the word ‘altogether.’ Views expressed in the examples do not represent the opinion of Merriam-Webster or its editors. Send us feedback.
Read Also: What Is The Geography Of Paraguay
What Are The Limitations Of Game Theory
Most economic problems involve many players. For instance, the number of sellers and buyers is quite large in monopolistic competition and the game theory does not provide any solution to it. Fifthly, even in its application to duopoly, game theory with its assumption of a constant-sum game is unrealistic.
Grade Levels And Timelines For Introducing Schemas
As mentioned previously, an attack strategy should be introduced and practiced alongside schema instruction. Attack strategies are relatively simple and can be learned quickly in contrast, understanding word-problem schemas and using a solution strategy associated with each schema requires complex reasoning and a detailed set of skills. Developing mathematical reasoning related to the schemas takes sustained instruction that often spans the entire school year.
Additive schemas appear in mathematics materials as early as kindergarten, but typical schema introduction for additive schemas may start in first grade and continue across the elementary grades, depending upon the prior knowledge of students. Within a school year, we recommend introducing the additive schemas separately and providing mixed schema practice as new schemas are modeled and practiced. Among the three additive schemas, we recommend teaching combine problems first. This is because, when solving for missing parts in combine problems, the conceptual basis is the same no matter which of the parts is missing. Thus, the combine problem type is a relatively easy schema for establishing an understanding of the conceptual and procedural aspects of schema instruction.
Don’t Miss: What Is Figure Ground Perception Psychology
Altogether In Examples From Wordnik
- Locke, in particular, ruined the term altogether in English philosophical literature, where it has ceased to possess any recognized definite meaning.
- I’m blessed if I can make it out — he’s dropped the title altogether, and now calls himself _Mister_ — I’ve forgotten for the moment the rest of it, but it is an English name.
- It may be affirmed that the writers of the age of Louis XIV would not have used these expressions: they would never have thought of using the word “equality” without applying it to some particular object and they would rather have renounced the term altogether than have consented to make a living personage of it.
- Shrinking from the term altogether is not what our educational system should be doing.
- Shrinking from the term altogether is not what our educational system should be doing.
- Shrinking from the term altogether is not what our educational system should be doing.
- Shrinking from the term altogether is not what our educational system should be doing.
- Asthma is unlikely to be a single disease, so we should abolish the term altogether, states an Edito …
- So erase those, and keep your eye out for another label altogether, one that we can put just a touch more trust into.
- So erase those, and keep your eye out for another label altogether, one that we can put just a touch more trust into.
Altogether Vs All Together
- Altogether means completely,all things considered, or on the whole.
- All together means everyone together or everything together.
Its often said that the whole isnt necessarily the sum of its parts. That maxim applies when you turn every day into everyday, and its the same when you turn all together into altogetheryou get something completely different.
Also Check: Is Psychology Major Capitalized
What Does As Much As Mean In Math
As much as means that quantities are being compared much is an adjective referring to quantity. So 60% as much as means for every hundred units of quantity in $30, the answer has sixty such units. So we could solve this as. $30 is thirty times a hundred cents, so the answer is thirty times sixty cents
Teaching What Each Schema Means
To explain the three components of effective schema instruction, we use the compare problem type, which is often the most difficult of the schemas for students to understand. Difficulty with the compare problem arises at least in part because its structure relies on subtraction that is conceptualized as a difference between two numbers. This is relatively or entirely unfamiliar to many students because subtraction is taught in schools primarily, or even exclusively, as taking away.
For Mrs. Frank, our special education teacher, her lessons goal is that students solve the problem introduced at the beginning of this article . Before jumping to solving this compare problem, Mrs. Frank first presents intact compare stories with no missing quantities using concrete objects and actual student names. For example, Mrs. Frank introduces the compare schema by asking two students, Tina and Seth, to stand back to back, as she says: Tina and Seth are students in my class. Tina is 43 inches tall. Seth is 48 inches tall. Seth is 5 inches taller than Tina. Mrs. Frank then puts the compare graphic organizer on the board and leads a discussion in which she models and explains how to identify the boxes into which the bigger, smaller, and difference numbers go. Students discuss filling in the graphic organizer with a variety of compare stories, while Mrs. Frank gradually transfers responsibility to the students, all the time providing corrective feedback.
Sample compare problem.
Recommended Reading: Holt Geometry Chapter 7 Test Answer Key