Find An Interquartile Range For An Odd Set Of Numbers: Alternate Method
As you may already know, nothing is set in stone in statistics: when some statisticians find an interquartile range for a set of odd numbers, they include the median in both both quartiles. For example, in the following set of numbers: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 some statisticians would break it into two halves, including the median in both halves:, This leads to two halves with an even set of numbers, so you can follow the steps above to find the IQR.
Watch the video for the steps.
How To Find Q2
The number which divides any data set into two halves is q2 of the data. In fact, it is the value of the median in an arranged data set. The second quartile calculator is the best way to avoid manual calculations however for doing it by hand have a look at the following example.
Example:
- 5
- Median: 5 therefore data will be: 4 and 7
- Thus, q2 for the above data set is: 5
- Whereas q1: 4
- Q3: 7
If the values of q1 and q3 are known, then interquartile range of the data can also be calculated.
- Interquartile range: q3 q1 = 7 4 = 3
Are You Ready For More
Here is the;five-number summary of the age distribution at another party of 21;people.
Minimum: 5 years; ; Q1:;6 years ; ; Q2:;27 years; ; Q3:;32 years; ;Maximum: 60 years
Read Also: Geometry Segment Addition Postulate Worksheet
How To Find Q1 And Q3
Quartile calculators and quartile formulas are the best ways to find it. However, have a look on following examples to know about how you can calculate q1, q2 and q3. First of all, you have to follow a certain set of rules:
- You have to arrange your data from lowest to highest order.
- Now you have to look for median. It will be q2.
- At median you have to split the ordered data into two halves or equal sets.
- Now the median of lower half of data will be q1 and median of upper half of the data will be q3.
If your given data set is present in even numbers, then the median will be the average of the central 2 values. You have to add these 2 values, and then divide the answer by 2. The final outcome will be median that splits your data set into lower and upper halves.
Example:
How do you calculate q1 and q3 for a given data set?
In simple terms, just enter the given data set into the upper and lower quartile calculator to determine the first quartile Q1 and third quartile Q3, and if you want to do it manually, then stick to the given steps:
Range And Interquartile Range
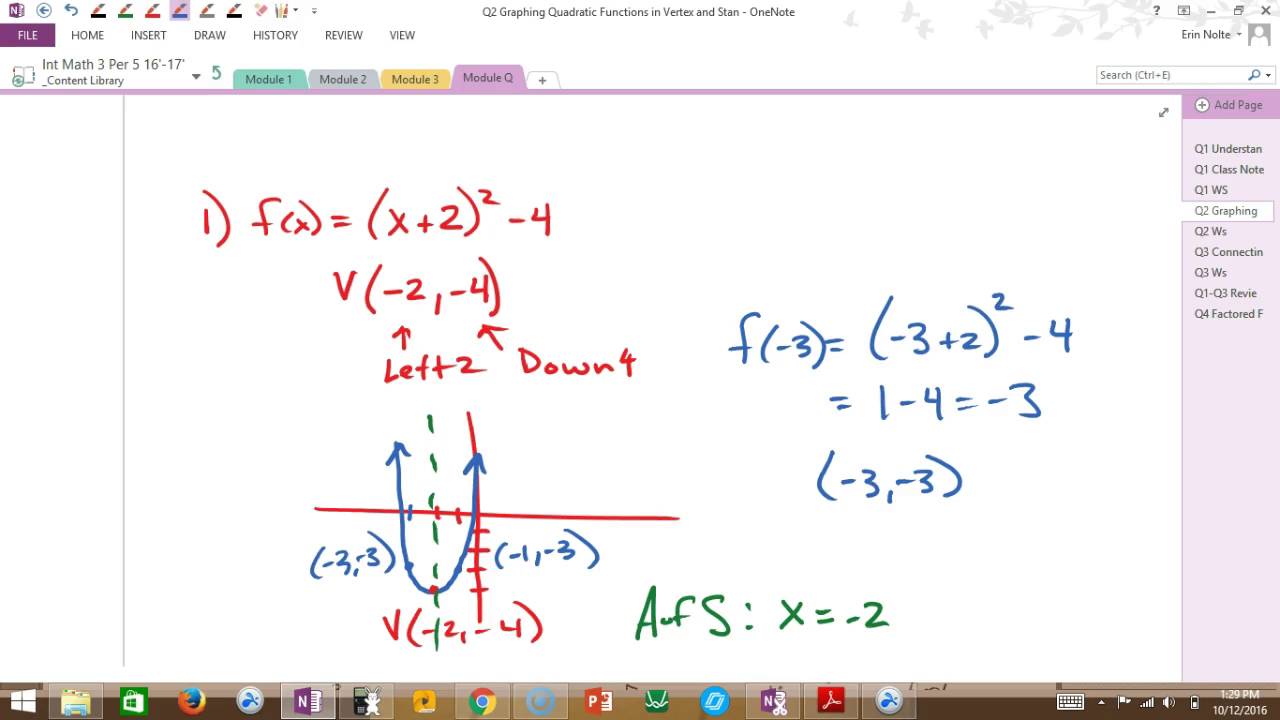
Here is a dot plot you saw in an earlier task. It shows how long Elenas bus rides to school took, in minutes, over 12 days.
Write the five-number summary for this data set by finding the minimum, Q1, Q2, Q3, and the maximum. Show your reasoning.
The range of a data set is one way to describe the spread of values in a data set. It is the difference between the greatest;and least;data values. What is the range of Elenas data?
Another number that is commonly used to describe the spread of values in a data set is the interquartile range , which is the difference between Q1, the lower quartile, and Q3, the upper quartile.
What is the interquartile range of Elenas data?
What fraction of the data values are between the lower and upper quartiles? Use your answer to complete the following statement:
The interquartile range is the length that contains the middle ______ of the values in a data set.
Here are two dot plots that represent two data sets.
Without doing any calculations, predict:
a. ;Which data set has the smaller IQR? Explain your reasoning.
b. ;Which data set has the smaller range? Explain your reasoning.
You May Like: What Is Copulation In Biology
Quartiles And Box Plots
Quartiles split a given a data set of real numbers x1, x2, x3 … xN into four groups, sorted in ascending order, and each group includes approximately 25% of all the data values included in the data set.Let Q1 be the lower quartile, Q2 be the median and Q3 be the be the upper quartile. The four groups of data values are defined by the intervals:Group 1: From the minimum data value to Q1 , Q1 is also called the 25th percentile because 25% of the data values in the data set are below Q1Group 2: From Q1 to Q2 , Q2 is also called the 50th percentile because 50% of the data values in the data set are below Q2Group 3: From Q2 to Q3 , Q3 is also called the 75th percentile because 75% of the data values in the data set are below Q3Group 4: From Q3 to maximum data value.
Notice And Wonder: Two Parties
Here are dot plots that show the ages of people at two different parties. The mean of each distribution is marked with a triangle.
Description:<p>Two dot plots from 5 to 45 by 5s. Age in years. Top dot plot labeled data set A. Bottom dot plot labeled data set B.There is a red triangle indicated at 15 on data set A and at 20 on data set B. The data for data set A are as follows: 8 years, 12 dots. 10 years, 3 dots. 12 years, 1 dot. 15 years, red triangle. 36 years, 1 dot. 42 years, 1 dot. 44 years, 2 dots. The data for data set B are as follows: 7 years, 1 dot. 8 years, 1 dot. 9 years, 1 dot. 10 years, 2 dots. 15 years, 1 dot. 16 years, 1 dot. 20 years, 2 dots and 1 red triangle. 22 years, 1 dot. 23 years, 1 dot. 24 years, 1 dot. 28 years, 1 dot. 30 years, 1 dot. 33 years, 1 dot. 35 years, 1 dot. 38 years, 1 dot. 42 years, 1 dot.</p>
What do you notice and what do you wonder about the distributions in the two dot plots?
Recommended Reading: What Is The Molecular Geometry Of Ccl4
Examples On Reading Quartiles From Box Plots
Example 3The box plots of the scores in an exam of classes A, B, C and D are shown below. The number of students in each of the classes A, B,C and D are 12, 19, 22 and 28 respectively.Use the box plots to answer the following questionsa) Determine the minimum and maximum scores, the lower and upper quartiles, the median, the range and interquartile range of each class.b) Which class has the highest score?c) Which class has the lowest score?d) How many students scored above the median in each class?e) How many students scored below the lower quartile in each class?f) How many students scored the lower quartile and the maximum in each class?h) Using the range and interquartile ranges, which class has the highest dispersion and which class has the lowest dispersion of scores?Solution to Example 3
How To Calculate Quartiles
If the size of the data set is odd, do not include the median when finding the first and third quartiles.
If the size of the data set is even, the median is the average of the middle 2 values in the data set. Add those 2 values, and then divide by 2. The median splits the data set into lower and upper halves and is the value of the second quartile Q2.
You May Like: Behaviorism Was Founded By
How Does This Quartile Calculator Work
This quartile calculator uses McCabe’s formula that does not take account of the median of the data set when computing the 1st and the 3rd quartiles.
Practically the 1st quartile is the median for the data set that contains all the values at the left of the 2nd quartile median, while the 3rd quartile is the median of the data set that contains all the values at the right of the 2nd quartile median.
As explained within instruction the number should be separated by commas, space or break line. For instance this data set: 1,2,3,4,5,6,7,8,9,10 and its results:
1st quartile = 3.25
2st quartile = 5.5
3st quartile = 7.75
Example 2 Range And Interquartile Range In Presence Of An Extreme Value
Find the range and interquartile range of the data set of example;1, to which a data point of value;75 was added.
The range would now be 69 . The median would be the mean of the values of the data point of rank;12 ÷ 2 = 6 and the data point of rank; + 1 = 7. Because it falls between ranks;6 and 7, there are six data points on each side of the median. The lower quartile is the mean of the values of the data point of rank;6 ÷ 2 = 3 and the data points of rank; + 1 = 4. The result is ;÷;2;=;25.5. The upper quartile is the mean of the values of data point of rank;6 + 3 = 9 and the data point of rank 6 + 4 = 10, which is ÷ 2 = 45. The interquartile range is 45;-;25.5;=;19.5.
In summary, the range went from 43 to 69, an increase of 26 compared to example 1, just because of a single extreme value. The more robust interquartile range went from 28 to 19.5, a decrease of only 8.5.
The second example demonstrated that the interquartile range is more robust than the range when the data set includes a value considered extreme. Its not a perfect measure, though. In this example, we might have expected that when adding an extreme value, the measure of dispersion would increase, but the opposite happened because there was a great difference between the values of data points of ranks;3 and 4.
Also Check: What Is The Molecular Geometry Of Ccl4
Box Plot Interquartile Range: How To Find It
Example question: Find the interquartile range for the above box plot.
- Step 1:Find Q1.Q1 is represented by the left hand edge of the box .
In the above graph, Q1 is approximately at 2.6.
- Step 2:Find Q3.Q3 is represented on a boxplot by the right hand edge of the box.Q3 is approximately 12 in this graph.
- Step 3:Subtract the number you found in step 1 from the number you found in step 3.This will give you the interquartile range. 12 2.6 = 9.4.
Thats it!
Watch the video for step-by-step directions:
Relevance And Uses Of Quartile Formula

As discussed above, the quartile formula helps us in dividing the data into four parts very quickly and eventually makes it easy for us to understand the data in these parts. For example, a class teacher wants to award the top 25% of students with goodies and gifts and wants to give another chance to bottom 25% of students to improve their score. He can use quartiles and can divide the data. So if the quartiles are said 51, 65, 72 and a student score is say 78, he will get goodies. If another student has a score of 48, he will another chance to improve the score, quick and easy interpretation.
Don’t Miss: What Does G Represent In Physics
How Do I Find The First Quartile
The first quartile, denoted by Q1, is the median of the lower half of the data set. This means that about 25% of the numbers in the data set lie below Q1 and about 75% lie above Q1. The third quartile, denoted by Q3, is the median of the upper half of the data set.
How To Find Median Quartiles And Percentiles
Example:Find the median, lower quartile and upper quartile of the following numbers. 12, 5, 22, 30, 7, 36, 14, 42, 15, 53, 25
Solution:First, arrange the data in ascending order:
Median = 22
Lower quartile = 12
Upper quartile = 36
If there is an even number of data items, then we need to get the average of the middle numbers.
Example:Find the median, lower quartile, upper quartile, interquartile range and range of the following numbers. 12, 5, 22, 30, 7, 36, 14, 42, 15, 53, 25, 65
Solution:First, arrange the data in ascending order:
Lower quartile or first quartile =
Median or second quartile =
Upper quartile or third quartile =
Interquartile range = Upper quartile lower quartile = 39 13 = 26
Range = largest value smallest value = 65 5 = 60
When evaluating the quartiles, always remember to first arrange the data in increasing order.
How to compute the interquartile range for a set of data?Remember to reorganize the data so that you can find the median values easier.
Median, Quartiles and Interquartile RangeHow to calculate median, quartiles and interquartile range for discrete data.
Recommended Reading: Geometry Segment Addition Postulate Worksheet
Interquartile Range In Minitab: Steps
Example question: Find an interquartile range in Minitab for the Grade Point Average in the following data set:Grade Point Average : 1, 1, 2, 2, 3, 3, 3, 4, 4, 5, 5, 5, 6, 6, 6, 7, 7, 8, 8.
Step 1: Type your data into a Minitab worksheet. Enter your data into one or two columns.
Step 2: then click Basic Statistics, then click Display Descriptive Statistics to open the Descriptive Statistics menu.
Step 3: and then click the Select button to transfer the variable name to the right-hand window.
Step 4:
Step 5: Check Interquartile Range..
Step 6: The IQR for the GPA in this particular data set is 1.8.
Thats it!
Tip: If you dont see descriptive statistics show in a window, click Window on the toolbar, then click Tile. Click the Session window and then scroll up to see your results.
How Do You Find Q1 And Q3 In Excel
To calculate Q3 in Excel, simply find an empty cell and enter the formula =QUARTILE. Again, replacing the array part with the cells that contain the data of interest. 3. Finally, to calculate the IQR, simply subtract the Q1 value away from the Q3 value.
You May Like: Eoc Fsa Practice Test Algebra 2 No Calculator Portion Answers
What Is The Mode If All Numbers Are The Same
Recognize that no mode exists for data sets in which every value occurs the same number of times. If the values in a given set all occur the same number of times, the data set has no mode because no number is any more common than any other. For instance, data sets in which every value occurs once have no mode.
What Is Lower Quartile And Upper Quartile Formula
1st quartile is also known as the lower quartile. 2nd quartile is the same as the median dividing data into 2 equal parts. 3rd quartile is also called the upper quartile. We find the median of the given data points. The median of the set of the data values towards the left of this median forms the lower quartile and the median of the set of data points towards the right of this median forms the upper quartile.; Using the quartile formula, the first quartile = /4)th;Term and;third quartile = /4)th;Term
Recommended Reading: Eoc Fsa Warm Ups Algebra 1 Answers
What Is Quartile Formula
The quartile formula helps to divide;a set of observations into 4 equal parts. The first quartile lies in the middle of the first term and the median. The median is the second quartile. The middle value lying between the median and the last term is the third quartile. Mathematically, they are represented as follows,
When the set of observations are arranged in ascending order the quartiles are represented as,
1st quartile is also known as the lower quartile. 2nd quartile is the same as the median dividing data into 2 equal parts. 3rd quartile is also called the upper quartile.
The interquartile range is calculated as Upper Quartile Lower Quartile.
What Is A Quartile In Math
quartilequartilequartile
Quartiles are the values that divide a list of numbers into quarters: Put the list of numbers in order. Then cut the list into four equal parts.In this case all the quartiles are between numbers:
Similarly, how do you find q1 and q3? Q1 is the median of the lower half of the data, and Q3 is the median of the upper half of the data. , | . Q1 = 7 and Q3 = 16. Step 5: Subtract Q1 from Q3.
Also asked, how do you find the first quartile?
The first quartile, denoted by Q1 , is the median of the lower half of the data set. This means that about 25% of the numbers in the data set lie below Q1 and about 75% lie above Q1 . The third quartile, denoted by Q3 , is the median of the upper half of the data set.
How do you find the interquartile range?
To find the IQR, start by arranging the numbers in your data set from lowest to highest. Then, divide your data set in half and find the median of both the lower and upper half. If you have an odd amount of numbers, don’t include the middle number.
Don’t Miss: What Is The Molecular Geometry Of Ccl4