What Is Law Of Conservation Of Momentum In Physics

Which Formula Can Be Used To Express The Law Of Conservation Of Momentum

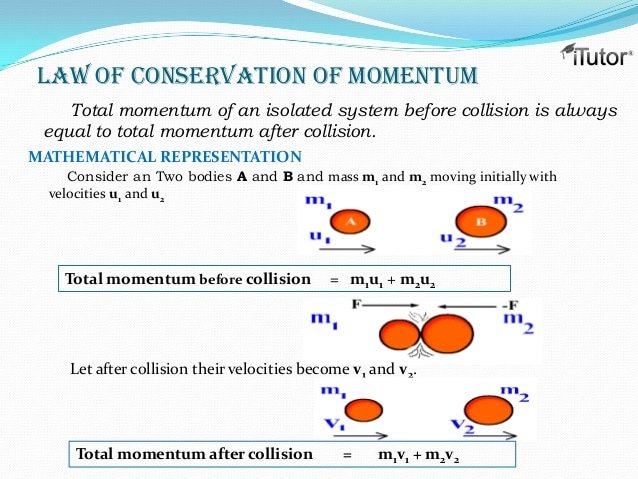
It is a physical quantity and the law of conservation of momentum says that for a collision occurring between object 1 and object 2 in an isolated system, the total momentum of the two objects before the collision is equal to the total momentum of the two objects after the collision. So simply it means that Pf = Pi.

Analogy To Linear Momentum

Angular momentum can be described as the rotational analog of linear momentum. Like linear momentum it involves elements of mass and displacement. Unlike linear momentum it also involves elements of position and shape.

Many problems in physics involve matter in motion about some certain point in space, be it in actual rotation about it, or simply moving past it, where it is desired to know what effect the moving matter has on the pointcan it exert energy upon it or perform work about it? Energy, the ability to do work, can be stored in matter by setting it in motiona combination of its inertia and its displacement. Inertia is measured by its mass, and displacement by its velocity. Their product,

\times & =}\\}\times }& =}\\m\times v& =p\\\end}}

is the matter’s momentum. Referring this momentum to a central point introduces a complication: the momentum is not applied to the point directly. For instance, a particle of matter at the outer edge of a wheel is, in effect, at the end of a lever of the same length as the wheel’s radius, its momentum turning the lever about the center point. This imaginary lever is known as the moment arm. It has the effect of multiplying the momentum’s effort in proportion to its length, an effect known as a moment. Hence, the particle’s momentum referred to a particular point,

(

m m} is the particle’s moment of inertia, sometimes called the second moment of mass. It is a measure of rotational inertia.

Error Analysis For Part A

If the conservation laws are correct, it is still unreasonableto expect the fractions calculated to have values of exactly one,because of experimental errors. Errors in length and time measurementswill have only a small effect on the results. The systematic errorcaused by friction Is more important. Once the losses are found,we will need to know how much can be attributed to friction beforeconcluding the conservation laws were not followed. The lossesdue to friction were calculated for the trials in part A . Although this will not give the exact errordue to friction, it should not be more than a few times larger.So, as long as the results differ from one by at most three orfour times the losses found for part A, we can assume those differencesare likely due to friction. Decide which conservation laws wereverified in each part.

You May Like: Founded Behaviorism

Three Application Of Conservation Of Momentum In Daily Life

• Air filled balloons

In the air-filled balloon, balloon, and air inside form a kind of system. Initially when the system is at rest, so the momentum of the system is also zero. As soon as the balloon is set free air escapes out with some great velocity, balloon moves forward in the direction opposite to air rushing out.

• The system of gun and bullet

Before firing both gun and bullet are at rest, therefore momentum of the system is zero. When the bullet is fired the bullet moves forward and gun recoils back. The mass of the gun is very large as compared to the mass of the bullet, therefore the recoils velocity is very small as compared to the velocity of the bullet.

• Motion of rockets and jet engines

Rockets and jet engines also work on the law of conservation of momentum. In these hot gases produced by burning of fuel rush out with large momentum, Due to this, these machines gain an equal and opposite momentum. This momentum enables the rockets and jet engines with very high velocities.

History Of The Concept

René Descartes believed that the total “quantity of motion” in the universe is conserved, where the quantity of motion is understood as the product of size and speed. This should not be read as a statement of the modern law of momentum, since he had no concept of mass as distinct from weight and size, and more important, he believed that it is speed rather than velocity that is conserved. So for Descartes if a moving object were to bounce off a surface, changing its direction but not its speed, there would be no change in its quantity of motion.Galileo, in his Two New Sciences, used the Italian word impeto to similarly describe Descartes’ quantity of motion.

Leibniz, in his “Discourse on Metaphysics“, gave an argument against Descartes’ construction of the conservation of the “quantity of motion” using an example of dropping blocks of different sizes different distances. He points out that force is conserved but quantity of motion, construed as the product of size and speed of an object, is not conserved.

You May Like: Define Span Linear Algebra

Objects Of Variable Mass

The concept of momentum plays a fundamental role in explaining the behavior of variable-mass objects such as a rocket ejecting fuel or a staraccreting gas. In analyzing such an object, one treats the object’s mass as a function that varies with time: m. The momentum of the object at time t is therefore p = mv. One might then try to invoke Newton’s second law of motion by saying that the external force F on the object is related to its momentum p by F = dp/dt, but this is incorrect, as is the related expression found by applying the product rule to

Requirements For Momentum Conservation

There is a complication, however. A system must meet two requirements for its momentum to be conserved:

A system of objects that meets these two requirements is said to be a closed system . Thus, the more compact way to express this is shown below.

Don’t Miss: Segment Addition Postulate And Midpoint Worksheet Answer Key

Angular Momentum In Nature And The Cosmos

Tropical cyclones and other related weather phenomena involve conservation of angular momentum in order to explain the dynamics. Winds revolve slowly around low pressure systems, mainly due to the coriolis effect. If the low pressure intensifies and the slowly circulating air is drawn toward the center, the molecules must speed up in order to conserve angular momentum. By the time they reach the center, the speeds become destructive.

Johannes Kepler determined the laws of planetary motion without knowledge of conservation of momentum. However, not long after his discovery their derivation was determined from conservation of angular momentum. Planets move more slowly the further they are out in their elliptical orbits, which is explained intuitively by the fact that orbital angular momentum is proportional to the radius of the orbit. Since the mass does not change and the angular momentum is conserved, the velocity drops.

Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite and the primary planet that it orbits . The gravitational torque between the Moon and the tidal bulge of Earth causes the Moon to be constantly promoted to a slightly higher orbit and Earth to be decelerated in its rotation. The Earth loses angular momentum which is transferred to the Moon such that the overall angular momentum is conserved.

Angular Momentum In Electrodynamics

When describing the motion of a charged particle in an electromagnetic field, the canonical momentumP is not gauge invariant. As a consequence, the canonical angular momentum L = r × P is not gauge invariant either. Instead, the momentum that is physical, the so-called kinetic momentum , is

p

Also Check: Are Michael Jacksons Kids His Biological Kids

Conservation In A Continuum

In fields such as fluid dynamics and solid mechanics, it is not feasible to follow the motion of individual atoms or molecules. Instead, the materials must be approximated by a continuum in which there is a particle or fluid parcel at each point that is assigned the average of the properties of atoms in a small region nearby. In particular, it has a density and velocity v that depend on time t and position r. The momentum per unit volume is v.

Consider a column of water in hydrostatic equilibrium. All the forces on the water are in balance and the water is motionless. On any given drop of water, two forces are balanced. The first is gravity, which acts directly on each atom and molecule inside. The gravitational force per unit volume is g, where g is the gravitational acceleration. The second force is the sum of all the forces exerted on its surface by the surrounding water. The force from below is greater than the force from above by just the amount needed to balance gravity. The normal force per unit area is the pressurep. The average force per unit volume inside the droplet is the gradient of the pressure, so the force balance equation is

. }\equiv }+\mathbf \cdot }\,.}

, p}}}=c^\nabla ^p\,,}

where c is the speed of sound. In a solid, similar equations can be obtained for propagation of pressure and shear .

The Meaning Of System

A system is the collection of objects in whose motion you are interested. If you are analyzing the bounce of a ball on the ground, you are probably only interested in the motion of the ball, and not of Earth thus, the ball is your system. If you are analyzing a car crash, the two cars together compose your system .

Also Check: Eoc Fsa Practice Test Algebra 1 No Calculator Portion

Application Of Law Of Conservation Of Momentum

Having said so the energy of a system is always conserved, one of the best applications of the law of conservation of momentum would be in space travel, there is no medium in space to exert a force on, then how do rockets travel?

Well, they eject matter at very high speed so in an isolated system the momentum should remain constant therefore the rocket will move in the opposite direction with the same momentum as that of the exhaust.

Stay tuned with BYJUS to know more about the law of conservation of momentum, Newtons Second Law of Motion, and much more.

Conservation Of Momentum Examples

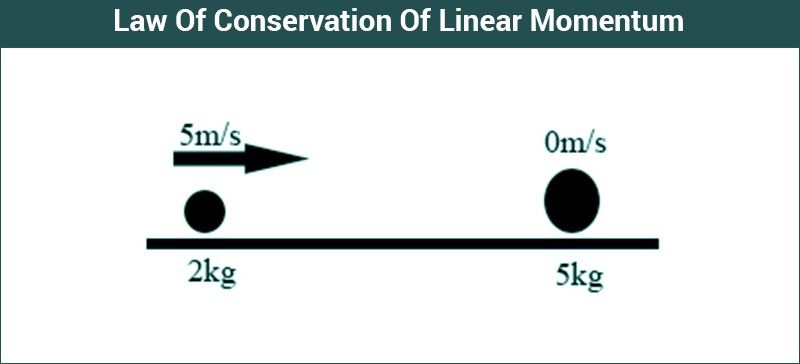
• Recoil of a Gun: If a bullet is fired from a gun, both the bullet and the gun are initially at rest i.e. the total momentum before firing is zero. The bullet acquires a forward momentum when it gets fired. According to the conservation of momentum, the gun receives a backward momentum. The bullet of mass m is fired with forward velocity v. The gun of mass M acquires a backward velocity u. Before firing, the total momentum is zero so that the total momentum after firing is also zero.

0 = mv + Mu

u is the recoil velocity of the gun. The mass of the bullet is much less than that of the gun i.e. m M. The backward velocity of the gun is very small,

u v

• Rocket Propulsion: Rockets have a gas chamber at one end, from which gas is ejected with enormous velocity. Before the ejection, the total momentum is zero. Due to the ejection of gas, the rocket gains a recoil velocity and acceleration in the opposite direction. This is a consequence of the conservation of momentum

If a rocket of mass m ejects the propellent of small mass dm with an exhaust velocity \ such that the residual rocket of mass m – dm acquires a velocity dv in the opposite direction, the momenta of the propellant and the residual rocket are equal in magnitude and opposite in direction.

Since both dmand dvare small, the equation can be approximated as

If the mass of the rocket reduces from \ to \ as its velocity increases from 0 to \, integrating the above equation

Also Check: Punchline Bridge To Algebra Answer Key Page 116

Closed And Isolated Systems

A closed system has no transfer of matter or net force with the outside world. An isolated system has no transfer of matter, net force, or energy with the outside world. Generally, we use closed systems in physics and isolated systems in thermodynamics.

These system types are important to understand because we study momentum problems in simplified versions of reality closed and isolated systems so that we only have to keep track of momentum within the system.

In real life, closed and isolated systems do not exist. Even if an object is placed in a remote spot in the vacuum of space, there will be small gravitational forces, electromagnetic energy exchange, and even occasional gas particles interacting with it.

However, we can study physics problems in the context of these systems. We can do so because, in certain situations, the forces, matter, and energy of the outside world are negligible, that is, their effect is so small and minuscule that they can be ignored.

Angular Momentum In Engineering And Technology

Examples of using conservation of angular momentum for practical advantage are abundant. In engines such as steam engines or internal combustion engines, a flywheel is needed to efficiently convert the lateral motion of the pistons to rotational motion.

Inertial navigation systems explicitly use the fact that angular momentum is conserved with respect to the inertial frame of space. Inertial navigation is what enables submarine trips under the polar ice cap, but are also crucial to all forms of modern navigation.

Rifled bullets use the stability provided by conservation of angular momentum to be more true in their trajectory. The invention of rifled firarms and cannons gave their users significant strategic advantage in battle, and thus were a technological turning point in history.

Newton, in the Principia, hinted at angular momentum in his examples of the First Law of Motion,

A top, whose parts by their cohesion are perpetually drawn aside from rectilinear motions, does not cease its rotation, otherwise than as it is retarded by the air. The greater bodies of the planets and comets, meeting with less resistance in more free spaces, preserve their motions both progressive and circular for a much longer time.

He did not further investigate angular momentum directly in the Principia,

However, his geometric proof of the law of areas is an outstanding example of Newton’s genius, and indirectly proves angular momentum conservation in the case of a central force.

Also Check: My Hrw Com Algebra 1

Procedure For Part B2

Make sure the apparatus is securely fastened and leveled ona block on the table. Latch the pendulum bob out of the way andpractice firing the ball from the gun out over the table. Notewhere the ball lands. Be careful of wild shots.

1) Tape a piece of white paper over the area of the table topwhere the ball lands. Cover it with carbon paper, carbon sidedown, so that the impact point of the ball will produce a mark.

2) With the ball in place and the gun released, find the positionon the table top directly below the center of the ball and markit with a piece of tape.

3) Measure the height from the bottom of the ball tothe table top.

4) Fire fiveshots, marking and numbering eachof the impacts.

5) Measure the range L of each of these shots from your tapemark.

Subatomic Collisions And Momentum

The conservation of momentum principle not only applies to the macroscopic objects, it is also essential to our explorations of atomic and subatomic particles. Giant machines hurl subatomic particles at one another, and researchers evaluate the results by assuming conservation of momentum .

Figure 3. A subatomic particle scatters straight backward from a target particle. In experiments seeking evidence for quarks, electrons were observed to occasionally scatter straight backward from a proton.

Also Check: Find Average Speed Physics