8the Polarization Of The Photon
The polarization vector eacts for the photon as the spin part of the wave function .
The various cases which can occur with regard to the polarization of the photon are identical with the possible types of polarization of a classical electromagnetic wave .
Any polarization ecan be represented as a superposition of two mutually orthogonal polarizations eand e e*= 0), chosen in some specified manner. In the resolution
The possibility that the photon has two different polarizations is equivalent to the statement that each eigenvalue of the momentum is doubly degenerate. This property is closely related to the fact that the mass of the photon is zero.
A freely moving particle with non-zero mass always has a rest frame. The intrinsic symmetry properties of the particle, as such, will evidently appear in this particular frame of reference. Symmetry with respect to all possible rotations about the centre must be considered. The property which describes the symmetry of the particle with respect to this group is its spin s this determines the degree of degeneracy, the number of different wave functions which are transformed into linear combinations of one another being 2s+ 1. In particular, a particle having a vector wave function has spin 1.
Thus the component of the photon angular momentum along the direction of its motion can have only the two values ±1 the value zero is not possible.
A.P. MillsJr., in, 1995
Helicity And Chirality In A Superposition Of Two Plane Waves
Perhaps the simplest case in which the polychromatic nature of an electromagnetic field can cause differences between the helicity and the chirality is a superposition of two co-propagating circularly polarised plane waves, of opposite handedness and different frequencies. This situation is considered in , and below a more detailed discussion is given.
For definiteness, let us consider the complex electric and magnetic fields given by
where E0 is the peak electric field amplitude of each plane wave, x and y are unit vectors and t z/c. This electromagnetic field is a superposition of a right-handed plane wave with frequency 1, and a left-handed wave with frequency 2. If the two frequencies are fairly close to one another, then the result can be viewed as a linearly polarised wave of frequency , with the plane of polarisation slowly rotating at a frequency . In this sense, it is like the static limit of the optical centrifuge discussed in in our case, the rotation does not accelerate.
As we are considering the free field, we may choose a gauge in which the scalar potential is 0, and use the relationships and
What Is Light Helicity
Helicity is a property of light which is familiar from particle physics but less well-known in optics. … We use a simple analogy between the helicity of light and electric charge and between the spin of light and electric current to demonstrate that the helicity is related to, but distinct from, the spin .
Also Check: Holt Mcdougal Geometry: Practice And Problem Solving Workbook Answer Key
What This All Has To Do With The Higgs
We have now learned that masses are responsible for mixing between different types of particles. The mass terms combine two a priori particles into a single particle . The reason why weve gone through this entire rigmarole is to say that ordinarily, two unrelated particles dont want to be mixed up into one another.
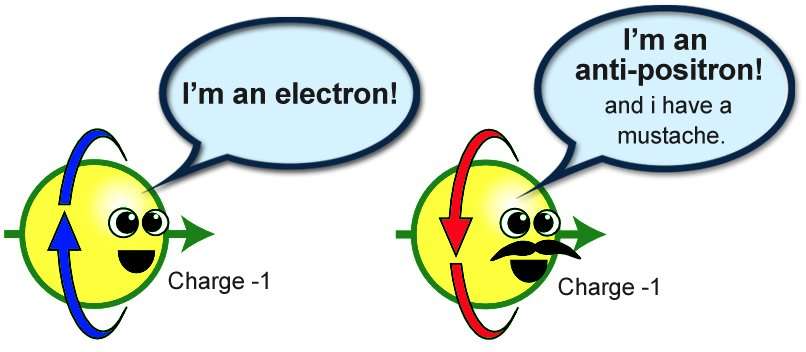
The reason for this is that particles can only mix if they carry the same quantum properties. Youll note, for example, that the electron and the anti-positron both had the same electric charge . It would have been impossible for the electron and anti-electron to mix because they have different electric charges. However, the electron carries a weak charge because it couples to the W boson, whereas the anti-positron carries no weak charge. Thus these two particles should not be able to mix. In highfalutin language, one might say that this mass term is prohibited by gauge invariance, where the word gauge refers to the W as a gauge boson. This is a consequence of the Standard Model being a chiral theory.
The reason why this unlikely mixing is allowed is because of the Higgs vev. The Higgs carries weak charge. When it obtains a vacuum expectation value, it breaks the conservation of weak charge and allows the electron to mix with the anti-positron, even though they have different weak charges. Or, in other words, the vacuum expectation value of the Higgs soaks up the difference in weak charge between the electron and anti-positron.
What Is Helicity And Chirality
Chirality and helicity The helicity of a particle is positive if the direction of its spin is the same as the direction of its motion. … The chirality of a particle is more abstract: It is determined by whether the particle transforms in a right- or left-handed representation of the Poincaré group.
Read Also: Define Abiotic Biology
Helicity Relativity And Mass
Now lets start to think about the meaning of mass. There are a lot of ways to think about mass. For example, it is perhaps most intuitive to associate mass with how heavy a particle is. Well take a different point of view that is inspired by special relativity.
A massless particle travels at the speed of light and you can never catch up to it. There is no rest frame in which a massless particle is at rest. The analogy for this is driving on the freeway: if you are driving at the same speed as the car in the lane next to you, then it appears as if the car next to you is not moving . Just replace the car with a particle.
On the other hand, a massive particle travels at less than the speed of light so that you can match its velocity so that the particle is at rest relative to you. In fact, you can move faster than a massive particle so that it looks like the particle is traveling in the opposite direction . Note that the direction of its spin does not change! However, we already noted that flipping only the particles directionand not its spinchanges the particles helicity:
Here weve drawn the particle with a blue arrow because it has gone from being right-handed to left-handed. Clearly this is the same particle: all that weve done is gone to a different reference frame and principles of special relativity say that any reference frame is valid.
Example: U And D Quarks In Qcd
Consider quantum chromodynamics with two masslessquarksu and d . The Lagrangian reads
- L
a b }_}^q_}^\rangle =v\delta ^} formed through nonperturbative action of QCD gluons, into the diagonal vector subgroup SUV known as isospin. The Goldstone bosons corresponding to the three broken generators are the three pions. As a consequence, the effective theory of QCD bound states like the baryons, must now include mass terms for them, ostensibly disallowed by unbroken chiral symmetry. Thus, this chiral symmetry breaking induces the bulk of hadron masses, such as those for the nucleons in effect, the bulk of the mass of all visible matter.
In the real world, because of the nonvanishing and differing masses of the quarks, SUL × SUR is only an approximate symmetry to begin with, and therefore the pions are not massless, but have small masses: they are pseudo-Goldstone bosons.
Also Check: Segment Addition Postulate Kuta
What Is Helicity Of Neutrino
The helicity of a particle is defined as the ratio ms/s, or the z-component of spin divided by the magnitude of the spin. By this definition in this case, the helicity is +1 for a right-handed antineutrino and -1 for a left-handed neutrino. Neutrinos as leptons. Role in supernova. Other neutrino types.
Appendix Exact Expressions For The Vector Potentials In A Chirped Pulse And An Optical Centrifuge
When considering chirped circularly polarised pulses in the body of the article, we made use of approximations to the vector potentials, and avoided explicitly evaluating the indefinite integrals and . Here we show an analytical method of treating these integrals. The integrals of and can be found using the standard integral
where the error function is defined by , and is extended to complex arguments by analytic continuation. With the identifications , and , we find the A potential associated with the chirped circularly polarised pulse of and to be
Corresponding results can be found for the C potential, and for down-chirped pulses or pulses of the opposite handedness. From these expressions for the potentials associated with chirped pulses, potentials corresponding to the optical centrifuge can also be straightforwardly obtained. Numerical values of the helicity density can be found by taking the real part of the complex potentials, using a series expansion for the complex error functions as given in .
For localised fields, this ambiguity is usually avoided by choosing the constant such that the potentials vanish at large distances . However, the expressions for the potentials given above do not approach 0 as approaches or
Don’t Miss: Algebra Nation Section 6 Test Yourself Answers
Helicity Chirality Mass And The Higgs
Weve been discussing the Higgs as part of our ongoing series on understanding the Standard Model with Feynman diagrams. Now Id like to take a post to discuss a very subtle feature of the Standard Model: its chiral structure and the meaning of mass. This post is a little bit different in character from the others, but it goes over some very subtle features of particle physics and I would really like to explain them carefully because theyre important for understanding the entire scaffolding of the Standard Model.
My goal is to explain the sense in which the Standard Model is chiral and what that means. In order to do this, well first learn about a related idea, helicity, which is related to a particles spin. Well then use this as an intuitive step to understanding the more abstract notion of chirality, and then see how masses affect chiral theories and what this all has to do with the Higgs.
What Is The Helicity Of A Particle At Rest
Given the definition of helicity as $\lambda = \vec \cdot \vec$ up to normalization, does it even make sense to define helicity for a particle at rest ?
If it doesn’t make sense, then what happens to the helicity of a state when it is boosted to its rest frame?
Edit:
The correct definition of helicity is $\lambda = \frac \cdot \vec}|}$.
To clarify my question, I have added more details here.
My question was due to some confusion in reading up on the helicity formalism from the book ‘Angular Momentum Techniques in Quantum Mechanics’ by Devanathan. This is discussed in chapter 13 of that book . The notation in that book for a helicity state is $\psi_$, where $p$ is the momentum and $\lambda$ is the helicity. Everything in that chapter seems fine up until Eq. given by
$\mathcal \psi_ = \eta \psi_$,
First, read up. The normalization is not irrelevant.
Helicity is defined as $\lambda =\hat \cdot \vec= \vec\cdot \vec/|\vec| ~,$ so for a massless particle, which has no rest frame, it is a relativistic invariant.
Putting it all together, first boost your particle to an infinitesimal momentum in its original direction. Then boost it to the opposite infinitesimal momentum so it has the opposite helicity. The helicity is then a step function of the momentum. What is the value at the midpoint of a step function, your 0/0, in your rest frame? 0? Note the spin in that frame is identical to the helicity in the upper, positive step of the step function.
Don’t Miss: Half Life Formula Chemistry Example
Scattering Amplitudes In Twistor Space
The scattering amplitude in QCD with n incoming gluons of the same helicity vanishes, as does the amplitude with n 1 incoming gluons of one helicity and one gluon of the opposite helicity for n 3. The first nonvanishing amplitudes are the maximal helicity violating amplitudes involving n 2 gluons of one helicity and two gluons of the opposite helicity. Stripped of the momentum conservation delta-function and the group theory factor, the tree-level amplitude for a pair of gluons of negative helicity is given by
Arun K. Majumdar, in, 2019
An Application In Particle Physics
In theoretical physics, the electroweak model breaks parity maximally. All its fermions are chiral Weyl fermions, which means that the charged weak gauge bosons W+ and W only couple to left-handed quarks and leptons.
Some theorists found this objectionable, and so conjectured a GUT extension of the weak force which has new, high energy W’ and Z’ bosons, which do couple with right handed quarks and leptons:
- S
This has two connected components where Z 2 _} acts as an automorphism, which is the composition of an involutiveouter automorphism of SUC with the interchange of the left and right copies of SU with the reversal of UBL . It was shown by Mohapatra& Senjanovic that left-right symmetry can be spontaneously broken to give a chiral low energy theory, which is the Standard Model of Glashow, Weinberg, and Salam, and also connects the small observed neutrino masses to the breaking of left-right symmetry via the seesaw mechanism.
In this setting, the chiral quarks
- (
Also Check: Cci4 Lewis Structure
Helicity And Chirality In An Optical Centrifuge
An optical centrifuge is a superposition of a left- and a right-handed circularly polarised plane wave, as in section 1, but with each wave linearly chirpedone chirped up and the other down. This means that the frequency difference between the two waves increases linearly with timeand so if the resulting superposition is viewed as linear polarisation with a rotating plane of polarisation, the angular speed of this rotation increases at a constant rate. These fields can be used to excite molecules to very high rotational states, and even dissociate heavy molecules. The action of an optical centrifuge in inducing molecular rotation can be analysed classically, as in the original paper of Karczmarek et al , or viewed quantum-mechanically as driving the molecules up a successive ladder of rotational transitions .
Because of this practical use, it seems worthwhile to extend the reasoning of sections 1 and 2 to examine the net helicity and chirality in such a field configuration. The fields of an optical centrifuge are given by the real parts of
From these, it is straightforward to find the chirality density
To find the helicity density, it is most straightforward to use the following approximations to the potentials, similar to the approximations made in section 2
We then find, using 3
The energy density in the centrifuge is given by
Orbital Angular Momentum For Atmospheric Free
Optical angular momentum is associated with the helicity photon wavefront and related to spatial distribution. Application of OAM beams in high data rate FSO communication has been explored recently . In order to fully utilize the terabit capacity of the optical carrier for potential FSO communication systems, research has been devoted to OAM-multiplexed free-space laser communication links. Increased capacity and spectral efficiency for high data rate communication are being studied using information carrying OAM beams, specifically for long distance, deep space, or near Earth optical communication for future potential technology. OAM for FSO applications is discussed in Ref. . As described in Ref. , the OAM transmitted beam can be expressed as follows:
L.D. LANDAU, E.M. LIFSHITZ, in, 1974
Read Also: Kuta Infinite Geometry
Worldsheet Of A Continuous Helicity Particle
D.S. Kaparulin, S.L. Lyakhovich, and I.A. Retuntsev
Phys. Rev. D 105, 065004 Published 4 March 2022
Abstract
We consider the class of spinning particle theories, whose quantization corresponds to the continuous helicity representation of the Poincare group. The classical trajectories of the particle are shown to lie on the parabolic cylinder with a lightlike axis irrespectively to any specifics of the model. The space-time position of the cylinder is determined by the values of momentum and total angular momentum. The value of helicity determines the focal distance of parabolic cylinder. Assuming that all the world lines lying on one and the same cylinder are connected by gauge transformations, we derive the geometrical equations of motion for the particle. The timelike world paths are shown to be solutions to a single relation involving the invariants of trajectory up to fourth order in derivatives. Geometrical equation of motion is non-Lagrangian, but it admits equivalent variational principle in the extended set of dynamical variables. The lightlike paths are also admissible on the cylinder, but they do not represent the classical trajectories of this spinning particle. The classical trajectories of massless particle are shown to lie on hyperplanes, whose space-time position depends on momentum and total angular momentum.
- Received 13 December 2021
APS and the Physical Review Editorial Office Continue to Support Researchers
What Is Helicity In Chemistry
What is Helicity? Helicity is the property of having a screw-type or spiral pattern. In molecules, there are two types of helices: A geometric helix exists when atoms in a molecule are arranged into a spiral pattern, such as in a DNA molecule. These helices may be smaller than a full helix turn, as in BINAP.
You May Like: Algebra And Trigonometry 3rd Edition Stewart Pdf Free
Design Parameters 3d Magnetic Simulations And Magnetic Measurements Of The Ok
Necessity of controllable polarization in OK-5 FEL including the switch of the helicity sign resulted in the choice of pseudo-helical wigglers. Table 1 shows the major parameters of the wigglers. Each pseudo-helical wiggler is composed of two planar wigglers shifted with respect to each other on a quarter of the period . Each component of the field, vertical and horizontal, is independently controlled by the current in the vertical and horizontal coils. The wiggler is assembled from four quadrants with the coils attached to the yoke . Each coil consists of four water-cooled copper buses surrounding the poles in a snake-like fashion . Two layers of the coil make one complete turn around each pole. The yoke is fabricated from soft low carbon steel. The accuracy of the wiggler assembly is about 20 m . The design of the wiggler provides for an adiabatic entrance into the periodic part of the wiggler.
Table 1. Parameters of the OK-5 wigglers
| Wiggler period w, cm |
| 4.04 |
Fig. 1. Cross-section of the wiggler quadrant. Dimensions are in mm.
Fig. 2. 3D model of the wiggler for the simulations . Round pole tips with cuts.