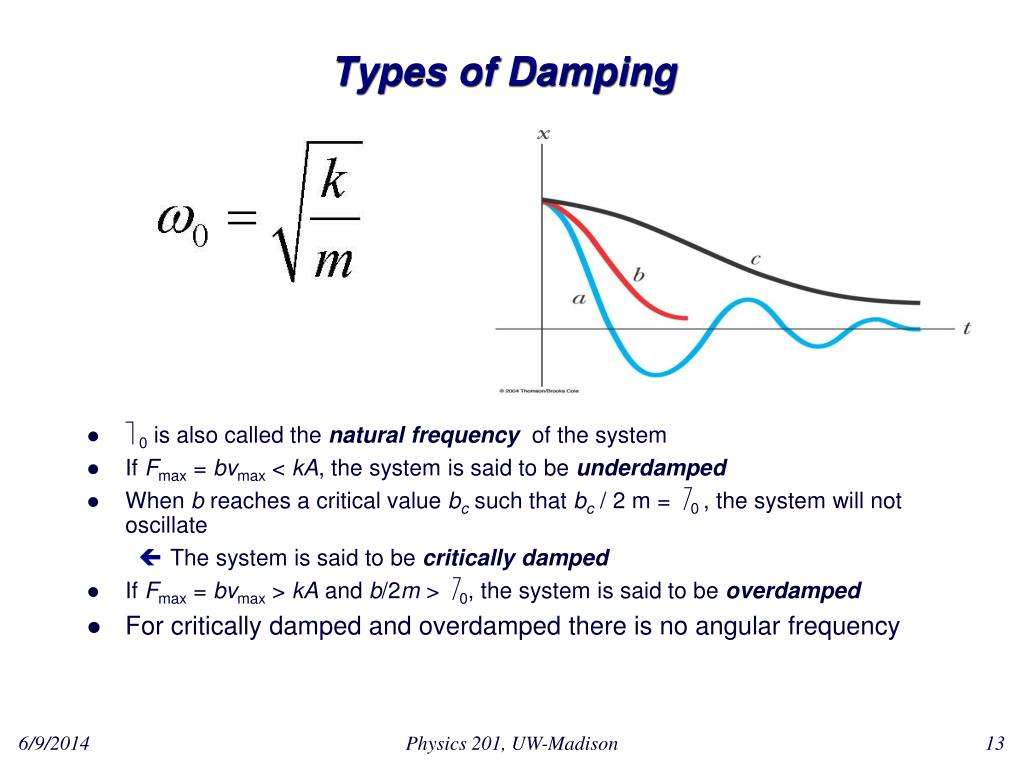
Shm Systems Under Damping
Damping changes the behaviour of S.H.M. systems. Certain features of the oscillation are dependent on the extent of damping.
An undamped system gives `normal’ S.H.M. – a sinusoidal trace – with constant amplitude – no energy transfer out of the sytem
In a lightly-damped system, the amplitude of oscillation decreases slowly as time goes on. An example of such a system would be a pendulum in a clock – air resistance causes the swing’s amplitude to decrease with time. the system suffers a steady drain of energy.
A heavily-damped system moves slowly until coming to rest. It does not oscillate but the governing equations are still the same. A spring-mass system immersed in a bath of very viscous liquid would be heavily-damped. Energy is drained from the system so that it takes longer to reach zero.
Critical damping causes a system’s amplitude to reach zero in the shortest time possible. Shock absorbers on cars are critically damped.
Damped Simple Harmonic Motion
When the motion of an oscillator reduces due to an external force, the oscillator and its motion are damped. These periodic motions of gradually decreasing amplitude are damped simple harmonic motion. An example of a damped simple harmonic motion is a simple pendulum.
In the damped simple harmonic motion, the energy of the oscillator dissipates continuously. But for a small damping, the oscillations remain approximately periodic. The forces which dissipate the energy are generally frictional forces.
What Is Torque Steer In Cars
Torque steer is a sensation that is commonly experienced in powerful front-wheel-drive cars. It happens under acceleration as the torque delivered by the engine overcomes the front tyres, resulting in either the steering wheel tugging in your hands, or the car pulling to one side of the road as you accelerate.
Also Check: Algebra Lineal Ejercicios Resueltos Numeros Complejos
Damping In Structural Dynamics: Theory And Sources
If you strike a bowl made of glass or metal, you hear a tone with an intensity that decays with time. In a world without damping, the tone would linger forever. In reality, there are several physical processes through which the kinetic and elastic energy in the bowl dissipate into other energy forms. In this blog post, we will discuss how damping can be represented, and the physical phenomena that cause damping in vibrating structures.
The Dependency Of Electromagnetic Damping
As the distance between the magnet and the conductor decreases, the damping force increases. The electromagnetic damping force is proportional to the induced eddy current, the magnetic field strength, and the speed of the object. This means that the faster the object moves, the greater the damping and the slower the motion of the lower object will be damping, which will result in a smooth stopping of the object.
You May Like: What Is On The Ap Biology Exam
More About Electromagnetic Damping
Students must have understood about Electromagnetic Damping through its detailed introduction and examples.
After studying about the theory attached to it and the procedure, students must have been able to strengthen their knowledge about the related concepts.
Sometimes, during the exam days, students often find it difficult to manage their time and figure out the technique that should be followed.
But, theres no one solution to it, everyone must have different habits and so, you can expect yourself to follow a schedule that your friend is following.
Read ahead to unlock some of the tips that you shall be following despite your personal interests and habits.
-
Identify and write down realistic goals: Realistic goals are the goals that are achievable if given a correct time frame, a good mindset, skills and abilities attached to it. These goals help you to not only get what you want but also what you can achieve. One should set these goals or targets very simple, which can be achieved without fail with little effort. It not only motivates oneself but also encourages to set new targets. The most important aspect that one should keep in their mind while setting the goals is better understanding of oneself, of one’s capabilities and one’s study pattern and then, nothing is unachievable.
What Affects The Damping Of A Spring
What variables affect the damping of a spring executing simple harmonic motion?
What are the independent variables, and what variables would need to be controlled in an experiment?
I’m attempting to complete an investigation where I measure the decrease in amplitude of a damped spring, and to prove the relationship between variables in the motion.
Thanks!
You should already be familiar with damping. It simply refers to the fact that if you set a spring going, it eventually stops.
The wikipedia article should cover most of what you want to know.
Any particular spring may be damped for all sorts of reasons. Any way the spring can lose energy contributes to damping, so it could be lost internally to heat due to stressing the material, or externally to heat via friction, or externally to an electromagnetic field, to some sort of mechanical dashpot, etc.
If you were designing an experiment to study damping, you could be interested in a number of different particular things. You will have to make your own choice about what the most interesting thing to study is. For example, would you like measure the damping ratio? The overall magnitude of the damping effect? The time it takes your spring to reduce its amplitude to 1/2 its previous value?
You May Like: How Are Biology And Technology Related
What Is The Purpose Of Rubber Draw Sheet In Perineal Care
A draw sheet is a small bed sheet placed crosswise over the middle of the bottom sheet of a mattress to cover the area between the persons upper back and thighs, often used by medical professionals to move patients. It can be made of plastic, rubber, or cotton, and is about half the size of a regular sheet.
Driven Oscillations And Resonance
Read Also: How To Improve Your Psychological Health
Properties And Methods Used To Cause Physical Objects To Resist Movement
Choose your operating system:
To slow down Physics Bodies, simulate atmospheric drag, or add resistance to a hinge, there are two properties available to Physics Bodies and Physics Constraints: Linear Dampingand Angular Damping. Linear Damping controls how much the Physics Body or Constraint resists translation, while Angular Damping controls how much they resist rotating.
What Is The Difference Between Damping And Friction
What is the difference between damping and friction? Both of them slows down any moving system. So what’s the conceptual difference between them?
- 1Sep 19, 2015 at 7:49
- 2$\begingroup$You’re right. From one point of view, friction is a particular type of damping. That said, in more advanced contexts people say “friction” to mean “damping”.$\endgroup$ DanielSankSep 19, 2015 at 7:52
- $\begingroup$Damping, as in your link, usually refers to the $x’$ term in $mx”-bx’-kx=0$ . It refers to viscous friction, either caused by hydraulics or air resistance. Friction, on the other hand, is independent of velocity and most often refers to the resistance between two solids moving against each other .$\endgroup$
They are entirely different concepts. Your question is like asking “What is the difference between “temperature” and “weather”?” The term “damping” in physics typically refers to an effect that causes a reduction in the rate at which some process takes place. For the case of harmonic motion this can result in a reduction of the amplitude of a harmonic oscillation. “Friction” typically refers to a force acting on a system. Friction can be the cause of damping in a system.
Also Check: Unit 1 Geometry Basics Homework 4
Solved Examples For You:
Q: When we immerse an oscillating block of mass in a liquid, the magnitude of damping will
a) decrease b) increase c) remain the same d) none of the above
Solution: b) The magnitude of damping will increase when we immerse the block in a liquid and its dissipation energy as well. Damping is proportional to the velocity of the block.
Damping Ratio Of Closed Loop System
To know the performance of damping ratio in closed-loop systems, one has to contemplate multiple scenarios which are given below:
The system has to be completely stable in the open-loop state when we consider Bode graphs
When the phase cross over frequency is more than gain cross over frequency, then the closed-loop system is considered to be stable
In the case of second-order systems, the damping ratio is nearly equivalent to the phase margin divided by 100 only when the phase margin value lies between 00 and 600. Here, the relation between settling time, bandwidth frequency, and damping ratio is
BW = n Ö
n = 4/ Ts
BW = 4/ Ts2 Ö
The below graph represents the relation between damping ratio and bandwidth frequency.
Damping Ratio v-s Bandwidth in Closed Loop
Read Also: What Is Goal Setting In Sport Psychology
What Is The Advantages Of Coil Spring
Coil springs allow the suspension system to flex much more than a leaf spring system does. This means that many high-performance trucks go for the coil spring suspension system rather than leaf spring. A coil system allows more movement in the suspension system, making them a better choice for difficult terrain.
Damping Ratio In Control System
In a control system, the order of the system is known by the power of the term s in the transfer functions denominator part. For instance, when the power of s is 2, then the order of the system is second order. The expression of the 2nd order control system is given by
C/R = n2/
Here corresponds to the damping ratio and n corresponds to the systems natural frequency.
C = R
With this, the time response of the 2nd order control system can be known.
To know the damping ratio and its performance in the second-order system, the time response has to be known and it is explained as follows:
To know this, the open-loop transfer function n2/ is connected with a feedback loop that has a gain of one.
The transfer function of a closed-loop control system with unity gain in the negative feedback loop is given by
C/R = G/
When the open loop transfer function is substituted, then
C/R = n2/
In the above equation, the power of s is two and so the system is termed a second-order system. The characteristic equation is
s2 + 2 ns + n2 = 0
s = -n ± n Ö
Considering the above equation, the damping ratio performance can be known,
- When the two roots are imaginary, then the damping ratio equals to 0
- When the two roots are real and equal, then the damping ratio equals to 1
- When the two roots are real but not complex, then the damping ratio is greater than 1
- When the two roots are complex, then the damping ratio lies between 0 and 1
Also Check: What Is Debriefing In Psychology
Short Intro To Electrostatic Waves
Without a magnetic field, in an electrostatic field you can consider the Vlasov equation and derive a dispersion relation for a wave,$$1 + \frac \int \frac dv_x = 0,$$where $\omega_e$ is the electron plasma frequency, $v_x$ is the x-velocity coordinate and $g$ is a 1d distribution that relates to the background distributions of all species .
You can see that this is quite complicated and contains a pole at $k v_x = \omega$. Anyway, using a bit of hand-wavy assumptions you can integrate this and arive at the Langmuir wave dispersion relation ,$$\omega^2 = \omega_e^2 + 3 k^2 v_e^2,$$where $v_e$ is the mean velocity of the electron species . This is basically a simple oscillation of the electrons with a frequency slightly higher than the electron plasma frequency.
How Is Damping Quantified
There are several ways by which damping can be described from a mathematical point of view. Some of the more popular descriptions are summarized below.
One of the most obvious manifestations of damping is the amplitude decay during free vibrations, as in the case of a singing bowl. The rate of the decay depends on how large the damping is. It is most common that the vibration amplitude decreases exponentially with time. This is the case when the energy lost during a cycle is proportional to the amplitude of the cycle itself.
A typical singing bowl. Image by Sneharamm0han Own work. Licensed under CC BY-SA 4.0, via Wikimedia Commons.
Lets start out with the equation of motion for a system with a single degree of freedom with viscous damping and no external loads,
After division with the mass, m, we get a normalized form, usually written as
Here, \omega_0 is the undamped natural frequency and \zeta is called the damping ratio.
In order for the motion to be periodic, the damping ratio must be limited to the range 0 \le \zeta < 1. The amplitude of the free vibration in this system will decay with the factor
where T0 is the period of the undamped vibration.
Another measure in use is the logarithmic decrement, . This is the logarithm of the ratio between the amplitudes of two subsequent peaks,
where T is the period.
The relation between the logarithmic decrement and the damping ratio is
Amplification for a single-DOF system for different frequencies and damping ratios.
Recommended Reading: What Does Y Mean In Math
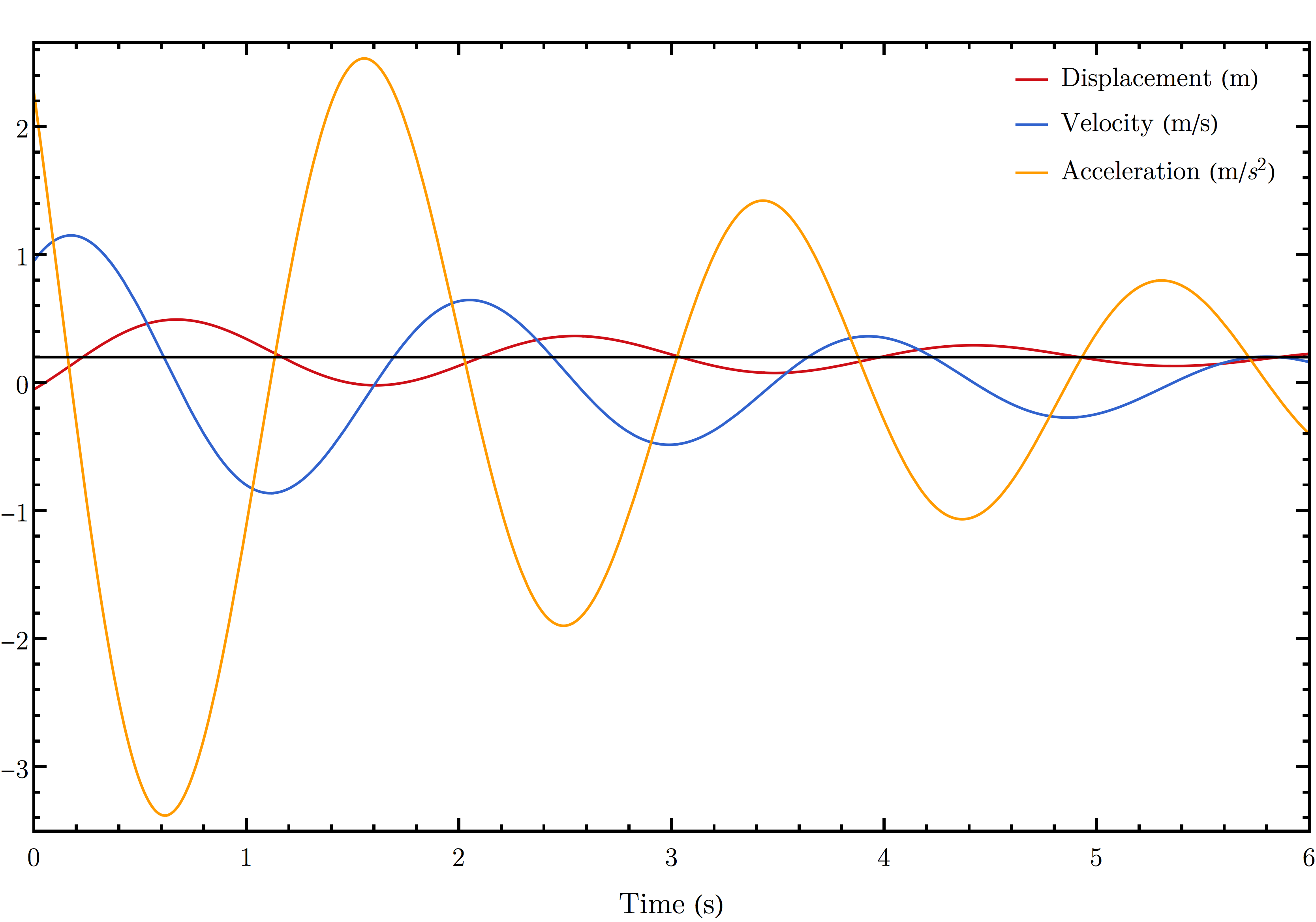
Expression Of Damped Simple Harmonic Motion
Lets take an example to understand what a damped simple harmonic motion is. Consider a block of mass m connected to an elastic string of spring constant k. In an ideal situation, if we push the block down a little and then release it, its angular frequency of oscillation is = k/ m.
However, in practice, an external force will exert a damping force on the motion of the block and the mechanical energy of the block-string system will decrease. This energy that is lost will appear as the heat of the surrounding medium.
The damping force depends on the nature of the surrounding medium. When we immerse the block in a liquid, the magnitude of damping will be much greater and the dissipation energy is much faster. Thus, the damping force is proportional to the velocity of the bob and acts opposite to the direction of the velocity. If the damping force is Fd, we have,
Fd = -b
where the constant b depends on the properties of the medium and size and shape of the block. Lets say O is the equilibrium position where the block settles after releasing it. Now, if we pull down or push the block a little, the restoring force on the block due to spring is Fs = -kx, where x is the displacement of the mass from its equilibrium position. Therefore, the total force acting on the mass at any time t is, F = -kx -b.
Now, if a is the acceleration of mass m at time t, then by Newtons Law of Motion along the direction of motion, we have
ma = -kx b
m + b + kx =0
x = Ae-bt/2m cos
=
What Is Damping Force
Damping force definition in physics is involved when vibrating motion is restrained, for example, alternating electric currents, noise, mechanical oscillations, by the energy being dissipated. It is an influence upon or in a system that is oscillating that results in the prevention or reduction of the motion of oscillation. When we talk about physical systems, this is a phenomenon that is a result of processes that end up dissipating energy. For example, a child moving to and fro in a swing the motion will die down due to damping if the child stops pushing the swing in either direction.
On the other hand, there can be systems so damped that there is no vibration at all. Critical damping is something that stops vibration or is just enough so that the object can return to the rest position as soon as possible. One example of this is the automobile shock absorber. Additional damping can result in overdamping, and this is necessary in some cases, like in door closers. For undamped systems, the vibrations eventually taper off to being nothing.
Some of the damping examples are carpet pads, vibrating springs, shock absorbers in automobiles, sounds produced by tuning forks over long distances, clock pendulum, oscillations of the branch of a tree, RLC circuits, etc. Friction affects damping as the relative motion between two surfaces pushing against each other to cause dissipation of energy. The kinetic energy in damping gets converted to heat by friction.
Recommended Reading: What Is The Right Hand Rule In Physics
What Is A Damping Text Books Say Damping Is Proportional To Velocity
- 139
- 1
- 2
- 5,067
- 10
- 893
- 3
- 2
krab said:…It can be a constant , proportional to velocity , or proportional to velocity squared . Usually only the middle one is called damping.
- 671
- 2
- #7
- 424
chandran said:What is a damping. Text books say damping is proportional to velocity. Why not damping is proportional force? or why not damping proportional to some other parameter. What does damping actually do ? Is there any practical application ?
A damped, driven oscillator is described by the equation :m \ddot – c \dot – kx = f_0 sin Here, c is called the damping coefficient, and accounts for dissipation in a non-ideal spring.
A damped, driven oscillator is described by the equation :m \ddot – c \dot – kx = f_0 sin Here, c is called the damping coefficient, and accounts for dissipation in a non-ideal spring.