How To Find Coplanar Points And Coplanar Lines
When looking for coplanar points and lines, its important to go back to the twos basic definitions. Heres a question guide to help you decide whether two or more points or lines are coplanar to each other:
- Do the lines lie on the same plane?
- Do the points lie on the same line?
If the answer is yes to either of the two questions, then they are coplanar. Start with a reference point or line, then look for another pair that lies along the same plane.
What Is The Best Definition Of A Coplanar
Lying or occurring in the same plane. Used of points, lines, or figures. adjective. In the same plane.
What does collinear and coplanar mean in geometry?
This means, that if you look at just two points, they are automatically collinear, as you could draw a line that connects them. Coplanar means lying on the same plane. Points are coplanar, if they are all on the same plane, which is a two- dimensional surface.
Area Of Triangle Method
As per the area of triangle method, if three points P,\),Q,\),R,\) are collinear, the area of the triangle formed by all three points P,\),Q,\), and R,\) will be zero.
\+x_\left+x_\left\right)\right|=0\)
Example:
Solution: Let’s take as ,\), as ,\), and as ,\) .
Substituting these value in the formula of area of the triangle:
\+x_\left+x_3\left\right)\right|=0 \\ A=\frac \mid)+1)+3 \mid=0 \\ A=\frac||=0 \\ Area=\frac|0|=0 \\ Area=0 \)
Hence, the points are collinear.
Don’t Miss: Core Connections Algebra Chapter 9
Coplanar Lines In Vector And Coordinate Geometry
We will be reintroduced to coplanar lines when we take advanced math classes involving equations in vector and cartesian forms.
- In vector form: If two nonparallel lines, $\boldsymbol = \boldsymbol + m\boldsymbol$ and $\boldsymbol = \boldsymbol + n\boldsymbol$ are coplanar, $$.
- In cartesian form: When the coefficients and their corresponding ratios determinant is zero, the lines are coplanar.
These are just a quick glimpse of how coplanar lines are applied in higher mathematics, but for now, lets focus on the geometric definition and properties of coplanar points and lines.
Lets try to check our knowledge of coplanar points and lines by trying these examples.
Example 1
Which of the following are not coplanar?
Solution
The first three choices all lie on the same plane.
- The compass contains all the line marks on one surface.
- Wallpapers are two-dimensional, so all the lines around and within it are coplanar.
- Coordinates on one plane are all coplanar points.
However, the lines on two different notebooks lie on two different surfaces, so they are not coplanar.
Example 2
True or False? Skew lines are coplanar. Justify your answer.
Solution
This statement is false. Recall that skew lines are lines that do not lie on the same plane, never intersect, or parallel. This means that skew lines arenever coplanar and instead are noncoplanar.
Example 3
Solution
What Is Coplanar And Noncoplanar
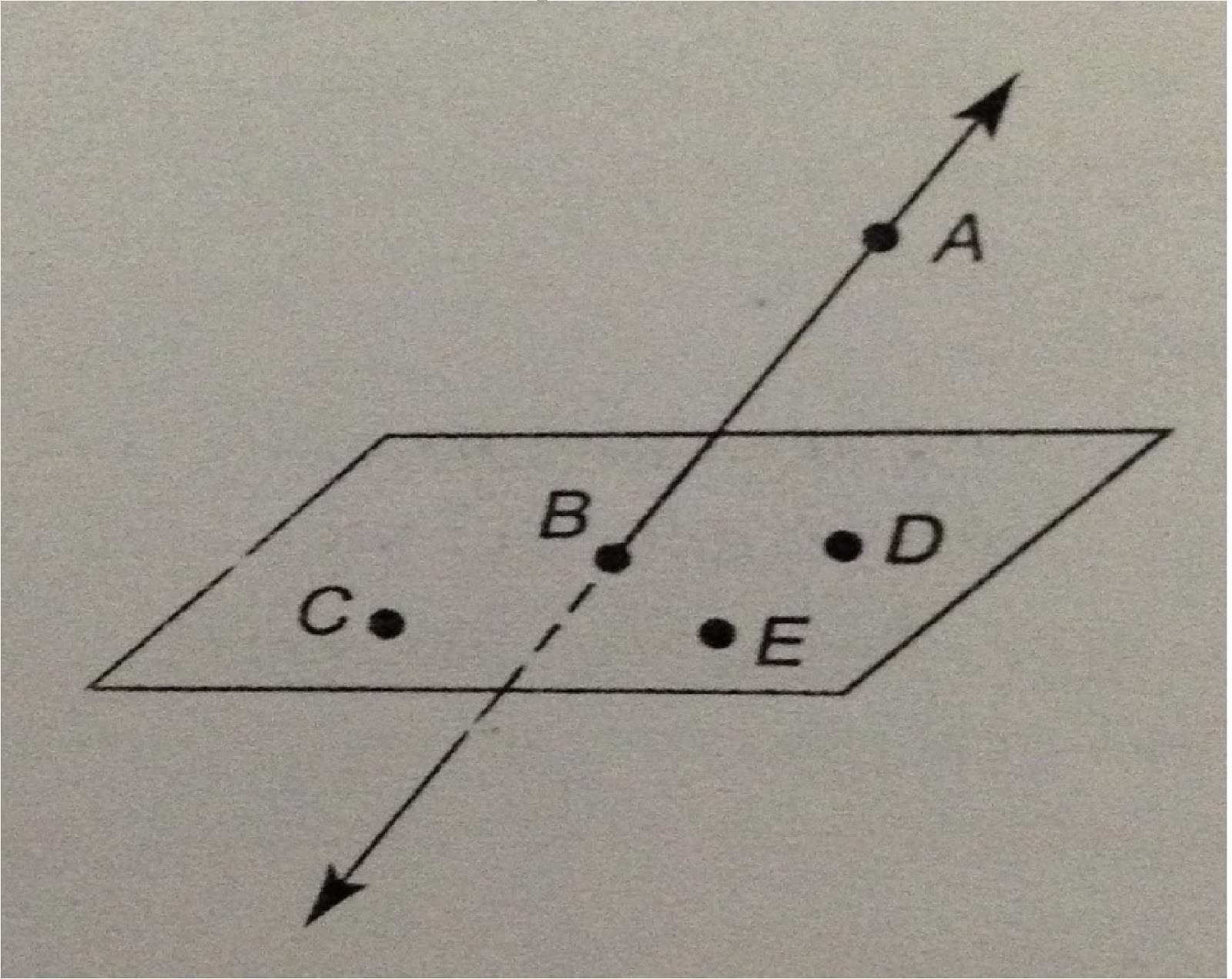
Coplanar points: A group of points that lie in the same plane are coplanar. Any two or three points are always coplanar. Non-coplanar points: A group of points that dont all lie in the same plane are non-coplanar. In the above figure, points P, Q, X, and Y are non-coplanar.
What does non coplanar mean in geometry?
: not occupying the same surface or linear plane : not coplanar two noncoplanar points.
Read Also: 4.5 Practice B Geometry Answers
Conditions For Coplanar Vectors/ Properties Of Coplanar Vectors
-
If three vectors are coplanar then their scalar product is zero, and if these vectors are existing in a 3d- space.
-
The three vectors are also coplanar if the vectors are in 3d and are linearly independent.
-
If more than two vectors are linearly independent then all the vectors are coplanar.
So, the condition for vectors to be coplanar is that their scalar product should be 0, and they should exist on 3d then these vectors are coplanar.
The equation system that has the determinant of the coefficient as zero is called a non-trivial solution. The equation system that has a determinant of the coefficient matrix as non zero, but the solutions are x=y=z=0 is called a trivial solution.
What Is The Definition Of Coplanar In Math
Definition Of CoplanarCoplanar
. Similarly, you may ask, what is the meaning of coplanar in math?
Coplanar Points: Definition. Coplanar points are three or more points which lie in the same plane. Recall that a plane is a flat surface which extends without end in all directions. It’s usually shown in math textbooks as a 4-sided figure.
Also, what is the opposite of coplanar? There are no categorical antonyms for coplanar. The adjective coplanar is defined as: Within the same plane.
Likewise, what is an example of coplanar?
Coplanar. Points or lines are said to be coplanar if they lie in the same plane. Example 1: The points P , Q , and R lie in the same plane A . They are coplanar .
What does it mean to be congruent?
Congruent. Angles are congruent when they are the same size . Sides are congruent when they are the same length.
Recommended Reading: What Happened To Beth Thomas Brother
What Is An Example Of Coplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique.
What are four coplanar points?
4 co-planar points are A, C, H, and F because they all occur on the rectangle/plane ACFD.
Coplanar Points Definition In Geometry
Four or more points that lie on the same plane are known as coplanar points. Remember that given any two points are always coplanar and given any three points are always coplanar. Here are some coplanar points examples from the above figure:
- A, B, C, and D are coplanar points.
- But each of F and E are NOT coplanar with A, B, C, and D.
- If any 3 points are taken at a time, a plane can pass through all those 3 points, and hence they are coplanar. For example:A, B, and E are coplanar.C, D, and F are coplanar.A, B, and E are coplanar, etc.
Recommended Reading: Countdown To The Algebra 1 Eoc Answer Key
What Are Coplanar Lines
Lines and line segments that lie on the same plane are considered coplanar lines.
The image above is a good example of a plane with three line segments coplanar to each other. $\overline$, $\overline$, and $\overline$ all lie on the same plane thats why they are coplanar lines.
Lets break down the important terms as well when learning about coplanar lines:
- line: a set of points that extend on both sides infinitely
- coplanar: when points or lines lie on the same plane, they are considered coplanar
- noncoplanar: when points or lines do not lie on the same plane, they are considered noncoplanar
What do we call lines that do not lie on the same plane? Lines that are not found on the same plane are called noncoplanar lines.
What Are Some Real
- The lines on a notebook are coplanar to each other.
- Since they lie on the same page, they lie on the same plane. Fun fact: not only are these lines coplanar, but they are also parallel.
Recommended Reading: Simplifying Radicals Worksheet Kuta
How Do You Prove Collinearity
As per theEuclidean geometry, a set of points are considered to be collinear, if they all lie in the same line, irrespective of whether they are far apart, close together, form a ray, a line, or aline segment. If you want to show that three points are collinear, choose two line segments, for example, PQ and QR. We, then, need to establish that they have a common direction and a common point . If both of these statements are true then the points can be considered as collinear.
Coplanar Lines Explanations & Examples
Determining whether two or more lines are coplanar lines will be helpful, especially when working with basic and coordinate geometry. Lets go ahead and recall its definition.
Coplanar lines are lines that lie on the same plane.
If coplanar points are pointsthat lie along the same plane, then the same applies for coplanar lines: they lie also share the same plane.
In this article, well dive into the fundamental definition of coplanar lines, their properties and learn how we can identify them from real-world examples.
Read Also: Error Of Parallax
What Are The 3 Defined Terms In Geometry
In Geometry, we have several undefined terms: point, line and plane. From these three undefined terms, all other terms in Geometry can be defined.
What is an example of a defined term?
A defined term is, simply put, a term that has some sort of definition. Unlike the and am, we can put a definition to the word she.She just is defined as a term that represents us acknowledging that someone is female.
Parallel Planes Don’t Count
In the deck of cards on the right none of the cards are coplanar.
Each card is in a plane of its own, and although those planes are parallel to each other, that does not count as being in the same plane. So in the deck we have 52 separate planes with one card in each plane.
To make the cards coplanar, you would have to lay them all out on a table with no overlaps.
Read Also: Child Of Rage Beth Today
It Only Really Applies To Four Points And Up
Any set of three points are always coplanar. Put another way, you can always find a plane that passes through any set of three points. Same for a set of two points.
This is similar to the idea that in two dimensions, two points are always collinear – you can always draw a line through any two points.
Coplanar And Non Coplanar Points
The points that lie on the same plane are called coplanar points and hence the points that do NOT lie on the same plane are called non-coplanar points. We know that two points in 2D can always pass through a line and hence any two points are collinear. In the same way, three points in 3D can always pass through a plane and hence any 3 points are always coplanar. But four or more points in 3D may not be coplanar. So we define the coplanar points and non-coplanar points as follows with respect to the following example:
You May Like: How Are Michael Jackson’s Kids White
Are All Parallel Lines Coplanar
Any two flat objects sharing space on a plane surface are said to be coplanar. Three types of lines that are coplanar are parallel lines, perpendicular lines, and transversals . These all exist in a single plane, unlike skew lines . Any two lines in a plane must necessarily either be parallel or intersect.
What Is The Difference Between Collinearity And Coplanarity
In geometry, three or more points are considered to be collinear if they all lie on a single straight line. This property of the points is called collinearity. On the other hand, three or more points are considered to be coplanar if they all lie in the same plane. This property of the points is called coplanarity.
Recommended Reading: What Are 4 Goals Of Psychology
What Is The Formula Of Collinearity
If P, Q, and R are three collinear points, then, PQ + QR = PR. Another formula that proves three points to be collinear is the area of a triangle formula. After substituting the coordinates of the given points in the formula, if the value is equal to zero, then the given points will be collinear. For example, if three points A , B and C are collinear, then = 0.
How To Determine Whether Given 4 Points Are Coplanar
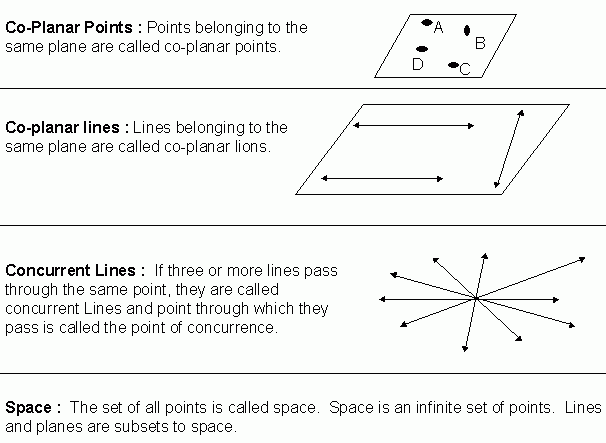
There are several methods to determine whether any 4 given points are coplanar. Let us learn each method. Consider the following example in each of the methods.
Example: Determine whether the four points A, B, C, and D are coplanar.
Method 1 for Determining Coplanar Points
For any four points to be coplanar, find the equation of the plane through any of the three points and see whether the fourth point satisfies it.
Let us first find the equation of the plane through the first three points:\\) =
– + = 0 – + = 0-8x + 8 – 4y – 4 + 4z – 8 = 0-8x – 4y + 4z – 4 = 0Divide both sides by -4,2x + y – z + 1 = 0
Now, we will substitute the fourth point = in it and see whether it is satisfied.2 + – 7 + 1 = 08 – 2 – 7 + 1 = 00 = 0, it satisfied.
Therefore, the given points are coplanar.
Method 2 for Determining Coplanar Points
For any given four points A, B, C, and D, find 3 vectors, say \, \, and \ to be coplanar see whether their scalar triple product is 0.
Let us find the vectors \, \, and \.
- \ = B – A = – =
- \= C – B = – =
- \ = D – C = – =
Now, their scalar triple product is nothing but the determinant formed by these three vectors. Let us find it and see whether it is 0.
\(\left|\begin
= 2 + 1 + 3 = 12 – 3 – 9
Therefore, the given four points are coplanar.
Method 3 for Determining Coplanar Points
For any given 4 points \\), \\), \\), and \\) to be coplanar, see if the 4×4 determinant \ is 0.
But this process may be difficult because calculating the 4×4 determinant is difficult.
Recommended Reading: Are Michael Jackson’s Kids Biological
What Is The Math Definition For Coplanar
DefinitionCoplanarCoplanar
. Also, what is an example of coplanar?
Coplanar. Points or lines are said to be coplanar if they lie in the same plane. Example 1: The points P , Q , and R lie in the same plane A . They are coplanar .
Subsequently, question is, what is the meaning of non coplanar points in math? The points which do not lie in the same plane or geometrical plane are called as non–coplanar points. Any 3 points can be enclosed by one plane or geometrical plane but four or more points cannot be enclosed by one. The points belong to the same plane are called as coplanar points.
Keeping this in view, how do you determine coplanar?
4 points are coplanar if the volume created by the points is 0. If any three points determine a plane then additional points can be checked for coplanarity by measuring the distance of the points from the plane, if the distance is 0 then the point is coplanar.
Are any two points coplanar?
Yes. In fact, since it is possible to draw a line or a plane through any pair of points, any two points are both collinear and coplanar. A plane CAN be created, therefore they are coplanar. The exicsten e of said line and plane is irrelevant.
Coplanarity Of Points In N Dimensions Whose Coordinates Are Given
Since three or fewer points are always coplanar, the problem of determining when a set of points are coplanar is generally of interest only when there are at least four points involved. In the case that there are exactly four points, several ad hoc methods can be employed, but a general method that works for any number of points uses vector methods and the property that a plane is determined by two linearly independent vectors.
In an n-dimensional space , a set of k points, are coplanar if and only if the matrix of their relative differences, that is, the matrix whose columns are the vectors p
- n ] x_-w_& x_-w_& \dots & x_-w_\\y_-w_& y_-w_& \dots & y_-w_\\z_-w_& z_-w_& \dots & z_-w_\\\end}}
is of rank 2 or less, the four points are coplanar.
In the special case of a plane that contains the origin, the property can be simplified in the following way:A set of k points and the origin are coplanar if and only if the matrix of the coordinates of the k points is of rank 2 or less.
Also Check: Quantum Physics Proves God
Properties In Three Dimensions
In three-dimensional space, two linearly independent vectors with the same initial point determine a plane through that point. Their cross product is a normal vector to that plane, and any vector orthogonal to this cross product through the initial point will lie in the plane. This leads to the following coplanarity test using a scalar triple product:
Four distinct points, x1, x2, x3 and x4 are coplanar if and only if,
- \cdot =0.}
which is also equivalent to
- \cdot =0.}
If three vectors a, b and c are coplanar, then if ab = 0 then
- \mathbf } +\mathbf } =\mathbf ,}
where ^ } } denotes the unit vector in the direction of a. That is, the vector projections of c on a and c on b add to give the original c.