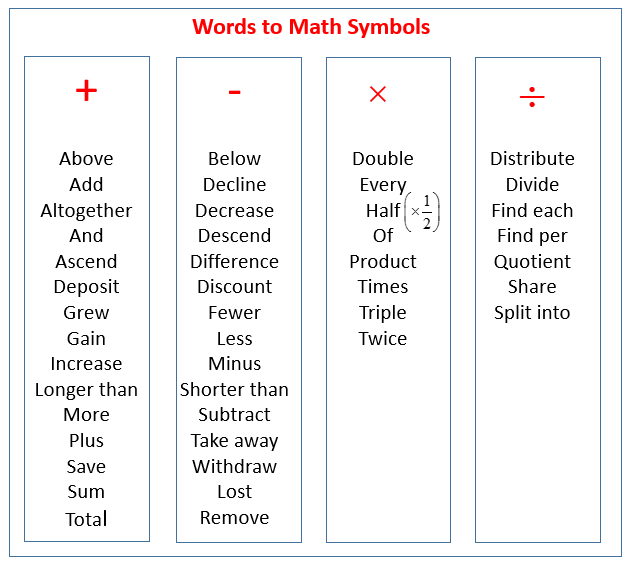
Addition And Subtraction Word Problem Keywords
- Each word problem contains numbers which should be written down.
- Keywords in the word problem can help us to decide whether to add or subtract these numbers.
- The list above contains some common addition and subtraction keywords.
- If you see these words in the word problem, they may help you to decide whether to add or subtract the numbers that you have already written down.
Write out the numbers given in the word problem text.
- Phoebe has 12 cm of ribbon and Jack has 23 cm of ribbon.
- How much ribbon do they have altogether?
- The word altogether tells us to add the two numbers to make a total.
- We can write the numbers of 12 and 23 with their digits above each other.
- Adding the units column, 2 + 3 = 5.
- Adding the tens column, 1 + 2 = 3.
- 12 + 23 = 35 and so, there is 35 cm of ribbon in total.
Whats Bigger Infinity Or Pi
Infinity is over 0, its over -284, its over 42, its over 4, its over 999,999,999,999,999,999*10^99999, its over a Googleplex, its even larger than a Googleplexian. Pi, on the other hand, is less than 4, its only 3.14159265 Since =C/d, pi is the ratio of a circles circumference to its diameter.
+ Addition Plus Positive
The addition symbol + is usually used to indicate that two or more numbers should be added together, for example, 2 + 2.
The + symbol can also be used to indicate a positive number although this is less common, for example, +2. Our page on Positive and Negative Numbers explains that a number without a sign is considered to be positive, so the plus is not usually necessary.
See our page on Addition for more.
You May Like: Which Founding Contributors To Psychology Helped Develop Behaviorism
The Meaning Of The Product Of A Number
The product of a number and one or more other numbers is the value obtained when the numbers are multiplied together. For example, the product of 2, 5 and 7 is
While the product obtained by multiplying specific numbers together is always the same, products are not unique. The product of 6 and 4 is always 24, but so is the product of 2 and 12, or 8 and 3. No matter which numbers you multiply to obtain a product, the multiplication operation has four properties that distinguish it from other basic arithmetic operations, Addition, subtraction and division share some of these properties, but each has a unique combination.
Math Is More Than Numbers

By Mathnasium | Added Jan 8, 2018
Using Math to Improve Important Life Skills
On the surface, math may seem like it’s all about numbers and formulas. However, this versatile subject is about much more than just counting, adding, and subtracting. Discover why math is more than numbers, and find out how it contributes to the development of valuable skills in problem solving, critical thinking, language, and more.
Problem-Solving Skills
Even simple addition and subtraction problems are about more than reaching the right answer. Both simple and complex math problems teach students important problem-solving skills that they can use for a variety of applications.
For example, complex word problems and algebra equations can help elementary to high school students understand and solve puzzles. While most word problems do require a combination of adding, subtracting, multiplying, and dividing, they also ask students to think through problems carefully. They require students to puzzle over relationships between people, the timing of events, and distances between locations. They can also encourage students to approach problems from a variety of perspectives.
Language Skills
Both elementary and high school students also have the opportunity to learn essential vocabulary in math class. Younger students may master the use of expressions, such as “less than” or “greater than,” while advanced students may learn entirely new vocabulary sets in geometry, algebra, or trigonometry class.
Recommended Reading: Segment Addition Postulate Worksheet Answers
The Arithmetic Property Of Commutation
Commutation means that the terms of an operation can be switched around, and the sequence of the numbers makes no difference to the answer. When you obtain a product by multiplication, the order in which you multiply the numbers does not matter. The same is true of addition. You can multiply 8 × 2 to get 16, and you will get the same answer with 2 × 8. Similarly, 8 + 2 gives 10, the same answer as 2 + 8.
Subtraction and division don’t have the property of commutation. If you change the order of the numbers, you’ll get a different answer. For example,
For subtraction,
Division and subtraction are not commutative operations.
What Does As Much As Mean In Math
As much as means that quantities are being compared much is an adjective referring to quantity. So 60% as much as means for every hundred units of quantity in $30, the answer has sixty such units. So we could solve this as. $30 is thirty times a hundred cents, so the answer is thirty times sixty cents
Recommended Reading: Fault Geography Definition
Operational Identities Difference And Sum Vs Product And Quotient
If you perform an arithmetic operation on a number and an operational identity, the number remains unchanged. All four basic arithmetic operations have identities, but they are not the same. For subtraction and addition, the identity is zero. For multiplication and division, the identity is one.
For example, for a difference, 8 0 = 8. The number remains identical. The same is true for a sum, 8 + 0 = 8. For a product, 8 × 1 = 8 and for a quotient, 8 ÷ 1 = 8. Products and sums have the same basic properties except that they have different operational identities. As a result, multiplication and its products have a unique set of properties that you have to know to get the right answers.
Related Articles
How Many More Meaning In Math
4.5/5how many morehow many moremathmoremeans
Math Operator-Vocabulary. Addition-sum, altogether, all, in all, together, total, total number, add, increase, increased by, more than. Subtraction-minus, greater than, take away, fewer than, less than, subtract, decreased by. Multiplication-product, multiply, multiplied by, times.
Likewise, does or mean add or multiply? Roughly speaking , in probability, the word or translates into addition, while and translates into multiplication. The added assumptions are: you can only add if the two events are disjoint. you can only multiply if the two events are independent.
Similarly one may ask, what operation is how many more?
The Basic Operations
Recommended Reading: Age Word Problems With Solutions
Subtraction Of Large Numbers
To subtract large numbers, list them in columns and then subtract only those digits that have the same place value.
Example 4
Find the difference between 7064 and 489.
Solution:
Note:
- Use the equals addition method or the .
- Line up the thousands, hundreds, tens and units place values for the two numbers when placing the smaller number below the larger number as shown above.
The Associative Property For Products And Sums
The associative property means that if you are performing an arithmetic operation on more than two numbers, you can associate or put brackets around two of the numbers without affecting the answer. Products and sums have the associative property while differences and quotients do not.
For example, if an arithmetical operation is performed on the numbers 12, 4 and 2, the sum can be calculated as
A product example is
But for quotients
and for differences
Multiplication and addition have the associative property while division and subtraction do not.
Read Also: What Does G Represent In Physics
Reducing Ambiguity By Agreement
In general, nobody wants to be misunderstood. In mathematics, it is so important that readers understand expressions exactly the way the writer intended that mathematics establishes conventions, agreed-upon rules, for interpreting mathematical expressions.
Does 10 5 3 mean that we start with 10, subtract 5, and then subtract 3 more leaving 2? Or does it mean that we are subtracting 5 3 from 10?Does 2 + 3 × 10 equal 50 because 2 + 3 is 5 and then we multiply by 10, or does the writer intend that we add 2 to the result of 3 × 10?
To avoid these and other possible ambiguities, mathematics has established conventions for the way we interpret mathematical expressions. One of these conventions states that when all of the operations are the same, we proceed left to right, so 10 5 3 = 2, so a writer who wanted the other interpretation would have to write the expression differently: 10 . When the operations are not the same, as in 2 + 3 × 10, some may be given preference over others. In particular, multiplication is performed before addition regardless of which appears first when reading left to right. For example, in 2 + 3 × 10, the multiplication must be performed first, even though it appears to the right of the addition, and the expression means 2 + 30.See full rules for order of operations below.
Introducing The Concept: Order Of Operations

Before your students use parentheses in math, they need to be clear about the order of operations without parentheses. Start by reviewing the addition and multiplication rules for order of operations, and then show students how parentheses can affect that order.
Materials: Whiteboard or way to write for the class publicly
Prerequisite Skills and Concepts: Students should be able to evaluate and discuss addition, subtraction, multiplication, and division expressions.
This would be a good moment to discuss the mathematical practice of attending to precision. In math, it is critical that we are deliberate when writing mathematical expressions and making mathematical statements. Small mixups with the math rules of operations or parentheses can cause drastic changes! Imagine incorrectly evaluating an expression when calculating a medicine dosage or a cost, for example.
Give students a few more examples, showing an expression with and without parentheses. Have student volunteers evaluate the expressions and compare their values. When students arrive at different values, avoid telling them they are right or wrong. Instead, have them find similarities and differences in their strategies, and guide the discussion so that students can see which strategy matches the rules for order of operations.
You May Like: Which Founding Contributors To Psychology Helped Develop Behaviorism
What Does Greater Than Mean In A Word Problem
wordsgreaterlessproblemless thanmeansless thanmeanslessmeansproblem
. Also asked, what does more than mean in word problems?
Addition-sum, altogether, all, in all, together, total, total number, add, increase, increased by, more than. Subtraction-minus, greater than, take away, fewer than, less than, subtract, decreased by. Multiplication-product, multiply, multiplied by, times.
Likewise, what words mean subtraction? The Basic Operations
| Symbol | |
|---|---|
| Addition, Add, Sum, Plus, Increase, Total | |
| Subtraction, Subtract, Minus, Less, Difference, Decrease, Take Away, Deduct | |
| × | Multiplication, Multiply, Product, By, Times, Lots Of |
| ÷ | Division, Divide, Quotient, Goes Into, How Many Times |
In this way, what does OFC mean?
Of Course
What are key words in word problems?
MathHelp.com
- Addition: increased by. more than. combined, together. total of.
- Subtraction: decreased by. minus, less. difference between/of. less than, fewer than.
- Multiplication: of. times, multiplied by. product of.
- Division: per, a. out of. ratio of, quotient of.
- Equals. is, are, was, were, will be. gives, yields. sold for, cost.
Or * Or Multiplication
These symbols have the same meaning; commonly × is used to mean multiplication when handwritten or used on a calculator 2 × 2, for example.
The symbol * is used in spreadsheets and other computer applications to indicate a multiplication, although * does have other more complex meanings in mathematics.
Less commonly, multiplication may also be symbolised by a dot . or indeed by no symbol at all. For example, if you see a number written outside brackets with no operator , then it should be multiplied by the contents of the brackets: 2 is the same as 2×.
See our page on Multiplication for more.
You May Like: Example Of Span Linear Algebra
What Does The 3 Mean In Math
In mathematics, the expression 3! is read as three factorial and is really a shorthand way to denote the multiplication of several consecutive whole numbers. Since there are many places throughout mathematics and statistics where we need to multiply numbers together, the factorial is quite useful.
< Less Than And > Greater Than
This symbol < means less than, for example 2 < 4 means that 2 is less than 4.
This symbol > means greater than, for example 4 > 2.
These symbols mean less than or equal to and greater than or equal to and are commonly used in algebra. In computer applications <= and >= are used.
These symbols are less common and mean much less than, or much greater than.
Also Check: Evaluating Functions Worksheet Algebra 2 Answer Key
Addition Of Large Numbers
To add large numbers, list them in columns and then add only those digits that have the same place value.
Example 2
Find the sum of 5897, 78, 726 and 8569.
Solution:
Note:
- Write the numbers in columns with the thousands, hundreds, tens and units lined up.
- 7 + 8 + 6 + 9 = 30.; Thus, the sum of the digits in the units column is 30.; So, we place 0 in the units place and carry 3 to the tens place.
- The sum of the digits in the tens column after adding 3 is 27.; So, we place 7 in the tens place and carry 2 to the hundreds place.
- The sum of the digits in the hundreds column after adding 2 is 22.; So, we place 2 in the hundreds place and carry 2 to the thousdands place.
Common Mathematical Symbols And Terminology: Maths Glossary
Mathematical symbols and terminology can be confusing and can be a barrier to learning and understanding basic numeracy.
This page complements our numeracy skills pages and provides a quick glossary of common mathematical symbols and terminology with concise definitions.
Are we missing something? Get it touch to let us know.
You May Like: Who Are Paris Jackson’s Biological Parents
What Comes First In Order Of Operations
Over time, mathematicians have agreed on a set of rules called the order of operations to determine which operation to do first. When an expression only includes the four basic operations, here are the rules:
When simplifying an expression such as \, first compute \ since the order of operations requires first evaluating any multiplication and division from left to right before evaluating addition or subtraction. In this case, that means first calculating \ followed by \. Once all multiplication and division have been completed, continue by adding or subtracting from left to right. The steps are shown below.
| \ | |
| \ | Because \ |
| \ | Because \ |
| \ |
Consider another expression as an example:
| \ | |
| \ | Because \, which is done first because multiplication and division are evaluated first. |
| \ | |
| \ | Because \ |
Sometimes we might want to ensure addition or subtraction is performed first. Grouping symbols such as parentheses \\), brackets \, or braces \, allow us to determine the order in which particular operations are performed.
The order of operations requires that operations inside grouping symbols are performed before operations outside them. For example, suppose there were parentheses around the expression 6 + 4:
| \ \times 7 – 3\) | |
| \ | Because \, which is done first because it’s inside parentheses. |
| \ | Because \, and there are no more parentheses to consider. |
| \ | Because \ |
Multiply Or Add First Teaching Order Of Operations Rules
When students in Grades 3 and up initially learn to add, subtract, multiply, divide, and work with basic numerical expressions, they begin by performing operations on two numbers. But what happens when an expression requires multiple operations? Do you add or multiply first, for example? What about multiply or divide? This article explains what order of operations is and gives you examples that you can also use with students. It also provides two lessons to help you introduce and develop the concept.
Key Standard:
- Perform arithmetic operations involving addition, subtraction, multiplication, and division in the conventional order, whether there are parentheses or not.
The order of operations is an example of mathematics that is very procedural. It’s easy to mess up because it’s less a concept you master and more a list of rules you have to memorize. But don’t be fooled into thinking that procedural skills can’t be deep! It can present difficult problems appropriate for older students and ripe for class discussions:
- Does the left to right rule change when the multiplication is implied rather than spelled out? or \\) instead of \ or \.)
- Where does factorial fall within the order of operations?
- What happens when you have an exponent raised to another exponent, but there are no parentheses?
Read Also: Geometry Seeing Doing Understanding Answer Key Pdf
Does Fewer Mean Add Or Subtract
AdditionaddSubtractiontake awayfewerlesssubtract
Yes, usually, “fewer” means subtraction, but some questions might try to trick you!
Furthermore, what does the word fewer mean in math? fewer trains were late Synonyms: few. a quantifier that can be used with count nouns and is often preceded by `a’; a small but indefinite number. less. a quantifier meaning not as great in amount or degree.
Similarly one may ask, does how many mean subtract?
Subtraction, Subtract, Minus, Less, Difference, Decrease, Take Away, Deduct. × Multiplication, Multiply, Product, By, Times, Lots Of. ÷ Division, Divide, Quotient, Goes Into, How Many Times.
How many more is add or subtract?
Addition-sum, altogether, all, in all, together, total, total number, add, increase, increased by, more than. Subtraction-minus, greater than, take away, fewer than, less than, subtract, decreased by. Multiplication-product, multiply, multiplied by, times.