What Does Expanded Form Mean In Math

Expanded Form Of A Number

We know that the number written as sum of the place-values of its digits is called the expanded form of a number.

In expanded form of a number, the number is shown according to the place values of its digits.

This is shown here:

In 2385, the place values of the digits are given below:

Hence, 2385 = 2000 + 300 + 80 + 5

Thus, 2000 + 300 + 80 + 5 is the expanded form of 2385.

Again,

Solved Examples on Expanded Form of a Number:

1. Write the expanded form for the number 70,39,41,295.

Solution:

Therefore, the expanded form of the number 70,39,41,295 is 70,00,00,000 + 00000000 + 3000000+ 900000 + 40000 + 1000 + 200 + 90 + 5.

2. Find the expanded form of 453169.

Solution:

Place values of digits 453169

So, 453169 = 400000 + 50000 + 3000 + 100 + 60 + 9

3. Write the number in figures and then in words for the following expanded form:

80000 + 8000 + 500 + 50 + 7Solution:80000 + 8000 + 500 + 50 + 7

= 88557

Eighty eight thousand five hundred fifty seven

100000 + 30000 + 2000 + 10 + 6Solution:100000 + 30000 + 2000 + 10 + 6 = 132016

One hundred thirty two thousand sixteen We can write the expanded form of numbers in different ways.

4. Write in expanded form: 28369

20000 + 8000 + 300 + 60 + 9

2 × 10000 + 8 × 1000 + 3 × 100 + 6 × 10 + 9 × 1

2 ten thousands + 8 thousands + 3 hundreds + 6 tens + 9 ones

419,247

400000 + 10000 + 9000 + 200 + 40 + 7

How To Write A Number In Expanded Form

To write a number in expanded form write the value of each non-zero digit in the number with addition signs between them.

The amount of numbers added together in the expanded form answer will be the same of the amount of non-zero digits in the original number.

Here is an example of writing the number 149 in expanded form.

We have 3 non-zero digits, which are 1, 4 and 9. This means that our expanded form answer will be made up of three numbers added together.

The value of each digit is equal to the digit multiplied by the value of the place value column it is in.

The 9 is in the ones column and 9 × 1 = 9. We just write 9.

The 4 is in the tens column and 4 × 10 = 40. The 4 is worth 40.

The 1 is in the hundreds column and 1 × 100 = 100. Therefore this 1 is worth 100.

149 is written in expanded form as 100 + 40 + 9.

The values of the digits are written in the same order as the original number and they all have addition signs between them.

For whole numbers, we can also see that the value of each digit is the same as taking the digit and replacing the digits to the right of it in the number with a zero.

For example, to find the value of the digit 1 in 149, replace the 4 and the 9 with zeros. The digit 1 in 149 is worth 100.

In this next example we will write the number 603 in expanded form.

We dont include any zeros in our number when writing it in expanded form.

The number 603 is made up of just two non-zero digits: 6 and 3.

The 0 is not worth anything so we do not write it.

One: Change Standard Form To Expanded Form

Read Also: Test Form 2b Answers Chapter 7

What Does Index Notation In Maths Mean

In math and computer programming, index notation is used to denote the elements of a series of numbers. The formalism of using indexes varies from topic to topic. In particular, there are different methods of referencing the elements of a list, vector, or matrix, depending on whether you are writing a formal mathematical paper for publication or writing a computer program.

Can You Shorten A Number In Expanded Form

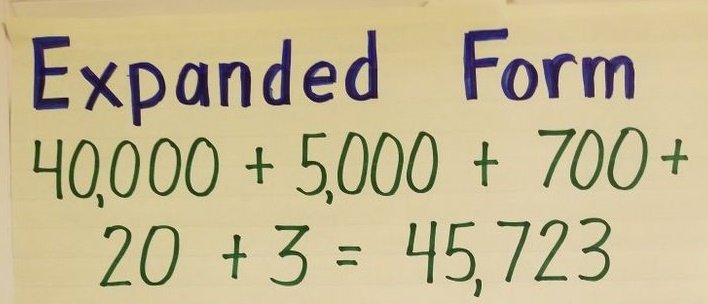
But the zero doesn’t affect the number in any way, because it doesn’t add any value. By writing numbers in expanded form, they didn’t have to worry about zeros. This means you can abbreviate the extended number to 4000 + 800 + 3. Converting numbers in reverse order from extended to standard is very easy.

Also Check: Ccl4 Vsepr Shape

Expanded Form With Decimals

A couple new issues arise when we include decimals, which are only mentioned in the archive in this question from 2001:

What is Expanded Notation?

We get more details in this unarchived question from 2010 explicitly about decimals:

My math assignment says I have to write expanded notation with numbers under 1, for example 0.05 and 0.7805How do you do it? Especially the zero's.0.00+0.050.000+0.7805Thanks Katie

The leading zeros might make a student trip up it appears that Katie is trying to include terms for them, which would be confusing. I answered:

Weren't you given any examples in class? Or is this an assignment to test what you already know, and you have never been taught this before? I'd like to have seen some attempt  in order to give me a better idea where to start.

Students do sometimes ask questions about topics they missed, or on tests not associated with what they have already learned its helpful when we can get such background information. Also, as weve seen, an example would clarify what kind of expanded form they are learning. Lacking that information, I offered several options:

There are slightly different ways to write "expanded notation", but one form is to show the value of each digit in the number, like this:  123 = 100 + 20 + 3or  123 = 1x100 + 2x10 + 3x1That is, the 1 means 1 hundred, so we write either 100 or 1x100. The 2 means 2 tens, so we write 20 or 2x10  and the 3 means 3 ones, so we write 3 or 3x1.

What Is The Expanded Form

The expanded form definition is the following:

Writing numbers in expanded form means showing the value of each digit. To be precise, we express the number as a sum of terms that correspond to the digit of ones, tens, hundreds, etc., as well as those of tenths, hundredths, and so on for the expanded form with .

As mentioned above, the expanded notation of, say, 154 should be a sum of terms, each connected to one of the digits. Obviously, we can’t just write 1 + 5 + 4 since that’s miles away from what we had. So how do you write a number in expanded form? Well, you add zeros.

154 = 100 + 50 + 4

So what does expanded form mean? Intuitively, we associate each digit of the number with something that has the same digit, followed by sufficiently many zeros to end up in the right position when we sum it all up. To make it more precise, let’s have it neatly described in a separate section.

Also Check: 4.5 Geometry Answers

What Does The Base Word Form Mean

In English grammar, the root is the form of a word to which prefixes and suffixes can be added to create new words. Instruction, for example, forms the basis for instructor training, instructor training and retraining. Also called root or trunk. In other words, basic forms are words that are not derivatives or constituents of other words.

Dont Abandon Expanded Form After The Unit 1 Test

Expanded form is too valuable to stop using after the place value unit ends. Two areas where expanded form supports increased understanding is with addition and decimals.

For addition, ask students to rewrite 34 + 128 in expanded form as 30 + 4 and 100 + 20 + 8 and illustrate the problem by drawing small circles for ones, rods for tens and squares for hundreds. Students benefit from using expanded form here because the emphasis remains on the place value of the numbers they are working with. The pictorial representation provides scaffolding for students who need something to help them count the sum.

You can also return to expanded form when teaching decimals. 4.72 rewritten as 4 + 0.7 + 0.02 highlights the value of each digit as students begin working with tenths and hundredths. Again, using visuals here will only strengthen student conceptualization of what it means to have two hundredths.

Of course, this is only the beginning of how expanded form can be used throughout the year. What are some of the ways you use expanded form in your math classroom?

Recommended Reading: Holt Mcdougal Geometry Answer Key

What Is The Difference Between Expanded Form And Standard Form

The standard form is the combination of digits written together as a single number. In the expanded form the digits of the number are split into each of the individual digits with their place value and written in expanded form. The example of standard form of a number is 4,982 and the same number can be written in expanded form as 4 × 1000 + 9 × 100 + 8 × 10 + 2 × 1 = 4000 + 900 + 80 + 2.

What Is The Difference Between Standard Expanded And Word Form In Math

When discussing integers, standard form refers to an integer written as a number, while word form describes an integer written out as a word. Expanded form uses different numbers in an equation to express the integer.

Examples of numbers written in standard form are 543 and 1,351. Standard form is the numerical form most often used in equations and general mathematics. Examples of numbers written in word form are twelve,five hundred forty-three and one thousand five hundred fifty-one. All compound numbers between 21 and 99 are hyphenated when written in word form. The word and is not necessary when writing out whole numbers it is necessary when writing out a number with digits to the right of a decimal point.

Expanded form consists of breaking down a number by degrees of place value. For example, the number 1,351 in expanded form is 1,000 + 300 + 50 + 1. Usually, the place values are arranged from greatest to least. Teachers typically use this form as a way to teach students about place value.

Standard form has a slightly different meaning in algebra. When referring to basic equations, standard form refers to an equation that equals zero. When referring to polynomials, standard form refers to arranging the terms from highest to lowest degree.

Don’t Miss: Holt Geometry Chapter 7 Test Form B Answer Key

What Does A Model Mean In Math

A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. A model may help to explain a system and to study the effects of different components, and to make predictions about behaviour.

What’s a number story?

A number story is a short story that illustrates a math equation, making it easier for young students to understand the equation involved. Some examples of number stories include: There were two children at home and then one went out to play.

How To Do Expanded Form

wikiHow is a wiki, similar to Wikipedia, which means that many of our articles are co-written by multiple authors. To create this article, volunteer authors worked to edit and improve it over time.There are 7 references cited in this article, which can be found at the bottom of the page. This article has been viewed 66,010 times.

Expanded form is a way to rewrite a numerical value that breaks up that value into separate digits, showing how much each digit actually represents in the process. Writing expanded form is fairly simple once you understand what it is.

You May Like: Edgenuity Economics Unit Test Answers

What Is Fully Factored Form

There is a fully factored form of this expression. Step-by-step explanation: Specified expression: You have to write the given expression in factored form and choose the correct one from the proposals. Factoring is the process of writing an expression as factors so that when multiplied, the same expression is obtained.

Two: Change Written Form To Expanded Form

Read Also: Nc To C Physics

How To Write Numbers In Expanded Form

Let’s take a number that has the form a…aaaaa, i.e., the a-s denote consecutive digits of the number with a being the ones digit, a the tens digit, and so on. According to the expanded form definition from the previous section, we’d like to write:

a…aaaaa = b + … + b + b + b + b + b,

with the number bcorresponding somehow toa.

Let’s explain how to write such numbers in expanded form starting from the right side, i.e., from a. Since it is the ones’ digit, it must appear at the end of our number. We create b by writing as many zeros to the right ofaas we have digits aftera in our number. In other words, we add none and get b = a.

Next, we have the tens digit a. Again, we form b by putting as many zeros to the right ofaas we have digits followinga in the original number. In this case, there’s one such , so we have b = a0 . Similarly, to bwe’ll add two zeros , meaning that b = a00, and so on until b = a00…000 with n-1 zeros.

Alright, we’ve seen how to write numbers in expanded form in a special case – when they’re integers. But what if we have ? Or if it’s some long-expression with several numbers before and after the dot? What is the expanded form of such a monstrosity?

Well, let’s see, shall we?

Write 5325 In Expanded Number Form

Standard Form:

5,000 + 300 + 20 + 5 = 5,325

Expanded Factors Form: + + + = 5,325

Expanded Exponential Form: + + + = 5,325

Word Form:five thousand, three hundred twenty-five

Note that in England and Great Britain the phrase “standard form” refers to the scientific number notation that the US calls “scientific notation.” Standard form in Great Britain and scientific notation in the US mean essentially the same thing when referring to the notation used to represent very large or very small numbers such as 4.959 × 1012 or 1.66 × 10-24.

Also Check: My Hrw Algebra 1

How To Write Decimals In Expanded Form

Essentially, we do the same as in the above section. In short, we again add a suitable number of zeros to a digit but for those after the decimal dot, we write them to the left instead of to the right. Obviously, the dot must be placed at the right spot so that it all makes sense . So how do you write a number in expanded form when it has some fractional part?

The framework from the first section doesn’t change: the expanded form with decimals should still give us a sum of the form:

a…aaaaa.ccc…c = b + … + b + b + b + b + b + d + d + d + … + d,

. Fortunately, we obtain b-s similarly as before we just have to remember to take the dot into account. To be precise, we add as many zeros as we have digits to the right, but before the decimal dot .

On the other hand, we find d-s by putting as many zeros on the left side of c-s as we have digits between the decimal dot and the digit in question.

For instance, to find d, we take c and add as many zeros as we have between the decimal dot andc . Then, we add the symbols0.at the very beginning, which gives d = 0.c. Similarly, we put one zero to the left of c , and obtain d = 0.0c. We repeat this for all d-s until d = 0.000…c, which has m-1 zeros after the decimal dot.

Let’s have an expanded form example with the number 154.102:

154.102 = 100 + 50 + 4 + 0.1 + 0.002.

10¹ = 10, 10² = 100, 10³ = 1000, 10¹ = 0.1, 10² = 0.01, 10³ = 0.001.