History Of Boolean Algebra
As mentioned earlier, Boolean algebra is invented in the year of 1854, by an English mathematician George Boole. He first stated the idea of the Boolean algebra in his book An Investigation of the Laws of Thought.
After this, the Boolean algebra is well known as the perfect way for representing the digital logic circuits.
In the late 19th century, scientists Jevons, Schroder and Huntington used this concept for modernized concepts. And in the year of 1936, M.H.Stone proved that the Boolean algebra is isomorphic to the sets .
In 1930s , a scientist named, Claude Shannon developed a new type algebra method as Switching Algebra by using the Boolean algebra concepts, for studying the switching circuits.
The logic synthesis of the modern electronic automation tools is efficiently represented by using Boolean functions known as Binary Decision Diagrams.
Boolean algebra allows only two states of a logic circuit, as True and False or High and Low or Yes and No or Open and Close or 0 and 1.
Boolean Expressions
These are similar to that of the mathematical expression. The Boolean expressions are formed by combining the logical variables by using the logical operators.;For example
- X +;Y
- X + Y
Subsets As Bit Vectors
A subset Y of X can be identified with an indexed family of bits with index setX, with the bit indexed by x X being 1 or 0 according to whether or not x Y. For example, a 32-bit computer word consists of 32 bits indexed by the set , with 0 and 31 indexing the low and high order bits respectively. For a smaller example, if X = where a, b, c are viewed as bit positions in that order from left to right, the eight subsets , , , , , , , and of X can be identified with the respective bit vectors 000, 001, 010, 011, 100, 101, 110, and 111. Bit vectors indexed by the set of natural numbers are infinite sequences of bits, while those indexed by the reals in the unit interval are packed too densely to be able to write conventionally but nonetheless form well-defined indexed families .
From this bit vector viewpoint, a concrete Boolean algebra can be defined equivalently as a nonempty set of bit vectors all of the same length and closed under the bit vector operations of bitwise , , and ¬, as in 10100110 = 0010, 10100110 = 1110, and ¬1010 = 0101, the bit vector realizations of intersection, union, and complement respectively.
Description Of The Laws Of Boolean Algebra
- Annulment Law A term ANDed with a 0 equals 0 or ORed with a 1 will equal 1
- A . 0 = 0;;;;A variable ANDed with 0 is always equal to 0
- A + 1 = 1;;;;A variable ORed with 1 is always equal to 1
Don’t Miss: What Is The Molecular Geometry Of Ccl4
A Brief Introduction To Switching Theory And Logic Design
- Professor at University of Massachusetts Lowell
Disclaimer
I’m still looking for a good application for drawing logic gates. The figures here are quite rough.
Early computers relied on many switches to perform the logical operations needed for computation. This was true as late as the 1970’s when early personal computers such as the Altair ) started to appear. Pioneering computer scientists such as Claude Shannon realized that the operation of these computers could be simplified by making use of an isomorphism between computer circuits and boolean algebra. The term Switching Theory was used at the time. Logical gates realized through increasingly smaller and smaller integrated circuits still perform the same functions as in early computers, but using purely electronic means. In this section, we give examples of some switching circuits. Soon afterward, we will transition to the more modern form of circuits that are studied in Logic Design, where gates replace switches. Our main goal is to give you an overview of how boolean functions corresponds to any such circuit. We will introduce the common system notation used in logic design and show how it corresponds with the mathematical notation of Boolean algebras. Any computer scientist should be familiar with both systems.
Note \
Many of the laws of Boolean algebra can be visualized thought switching theory. For example, the distributive law of meet over join is expressed as
Example \: Simplification of a Circuit
Example \
The Switching Theory Of A Switch
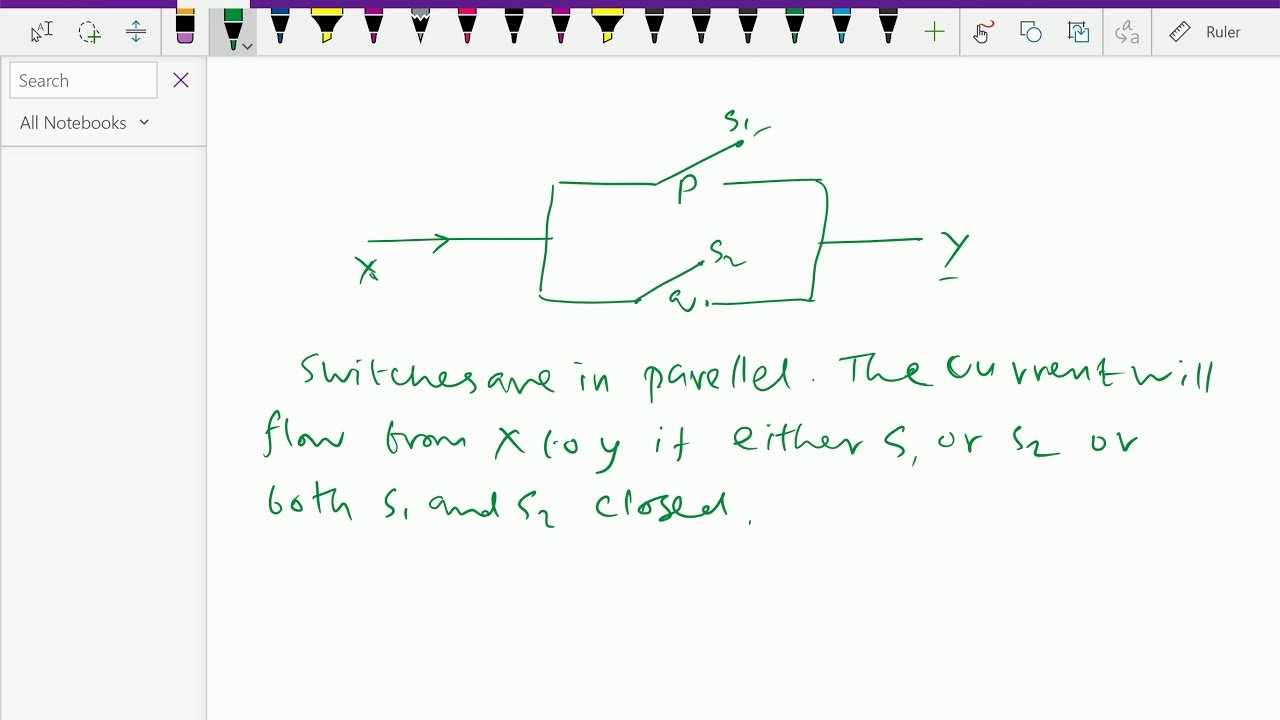
You may think that a switch is, well a switch, that can be used to turn a lighting load ON or OFF. But a switch can also be a complex mechanical or electromechanical element used to control the flow of a signal through it in either direction, making it a bilateral device. Consider the circuit shown.
Recommended Reading: Draw The Lewis Structure For Ccl4.
Simplification Of Boolean Functions
The K-map method is very easy to simplify a function than using identities. If n is the number of variables, then the K- map consists of 2n cells and there will be no similar value for any of the two adjacent rows of columns.
Frequently Asked Questions On Logic Gates
Q.1. Write the Boolean expression for AND gate.Ans: If \ and \ are the input, then the AND gate output can be given as \.
Q.2: Define logic gates.Ans: Logic gates are the digital circuits used to perform logical operations on the input applied across them and provide suitable output.
Q.3. What are universal gates? Give examples.Ans: Universal gates are designed by combining two or more basic gates to perform a certain logical operation. NAND and NOR gates are known as universal gates.
Q.4. If the input 0;is applied on a NOT gate, what will be the output?Ans: Since NOT gate is an invertor. Thus, if \;is applied at the input, the output will be \.
Q.5. Write the Boolean expression for OR gate.Ans: If \ and \ are the input, then the OR gate output can be given as \.
Q.6. Which logic gate is known as invertor?Ans: NOT gate is known as an invertor. The output obtained is the reverse of the input.
<script type="application/ld+json"></script>
Read Also: Algebra 1 Age Word Problems
Boolean Circuit Simplification Examples
- 7 – Boolean Algebra
- Boolean Circuit Simplification Examples
Lets begin with a semiconductor gate circuit in need of simplification. The A, B, and C input signals are assumed to be provided from switches, sensors, or perhaps other gate circuits. Where these signals originate is of no concern in the task of gate reduction.
Our first step in simplification must be to write a Boolean expression for this circuit. This task is easily performed step by step if we start by writing sub-expressions at the output of each gate, corresponding to the respective input signals for each gate.
Remember that OR gates are equivalent to Boolean addition, while AND gates are equivalent to Boolean multiplication.
For example, Ill write sub-expressions at the outputs of the first three gates:
. . . then another sub-expression for the next gate:
Finally, the output is seen to be equal to the expression AB + BC:
Now that we have a Boolean expression to work with, we need to apply the rules of Boolean algebra to reduce the expression to its simplest form :
The final expression, B, is much simpler than the original, yet performs the same function. If you would like to verify this, you may generate a truth table for both expressions and determine Qs status for all eight logic-state combinations of A, B, and C, for both circuits. The two truth tables should be identical.
The next step in evaluating the expression B is to multiply the signal B by the output of the previous gate :
Review
The Prototypical Boolean Algebra
The set and its Boolean operations as treated above can be understood as the special case of bit vectors of length one, which by the identification of bit vectors with subsets can also be understood as the two subsets of a one-element set. We call this the prototypical Boolean algebra, justified by the following observation.
- The laws satisfied by all nondegenerate concrete Boolean algebras coincide with those satisfied by the prototypical Boolean algebra.
This observation is easily proved as follows. Certainly any law satisfied by all concrete Boolean algebras is satisfied by the prototypical one since it is concrete. Conversely any law that fails for some concrete Boolean algebra must have failed at a particular bit position, in which case that position by itself furnishes a one-bit counterexample to that law. Nondegeneracy ensures the existence of at least one bit position because there is only one empty bit vector.
The final goal of the next section can be understood as eliminating “concrete” from the above observation. We shall however reach that goal via the surprisingly stronger observation that, up to isomorphism, all Boolean algebras are concrete.
Recommended Reading: Algebra 1 Age Word Problems
Truth Tables For The Laws Of Boolean
| Boolean | ||
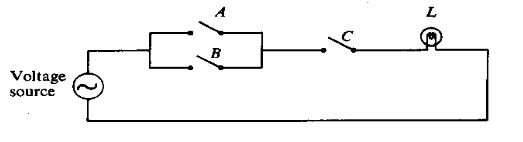
| A in parallel with closed= “CLOSED” | ||
| A in parallel with open= “A” | ||
| A in series with closed= “A” | ||
| A in series with open= “OPEN” | ||
| A in parallel with A = “A” | Indempotent | |
| A in series with A = “A” | Indempotent | |
| A in parallel with not A= “CLOSED” | ||
| A in series with not A= “OPEN” | ||
| A in parallel with B =B in parallel with A | Commutative | |
| A in series with B =B in series with A | Commutative | |
| invert and replace OR with AND | ; | |
| invert and replace AND with OR | ; | de Morgans Theorem |
Laws of Boolean AlgebraCommutative LawAssociative Lawdistributive LawLaws of Boolean
Section137a Brief Introduction To Switching Theory And Logic Design
Disclaimer: I’m still looking for a good application for drawing logic gates. The figures here are quite rough.
Early computers relied on many switches to perform the logical operations needed for computation. This was true as late as the 1970’s when early personal computers such as the Altair started to appear. Pioneering computer scientists such as Claude Shannon realized that the operation of these computers could be simplified by making use of an isomorphism between computer circuits and boolean algebra. The term Switching Theory was used at the time. Logical gates realized through increasingly smaller and smaller integrated circuits still perform the same functions as in early computers, but using purely electronic means. In this section, we give examples of some switching circuits. Soon afterward, we will transition to the more modern form of circuits that are studied in Logic Design, where gates replace switches. Our main goal is to give you an overview of how boolean functions corresponds to any such circuit. We will introduce the common system notation used in logic design and show how it corresponds with the mathematical notation of Boolean algebras. Any computer scientist should be familiar with both systems.
The standard notation used for Boolean algebra operations in switching theory and logic design is \ for join, instead of \ and \ for meet, instead of \ Complementation is the same in both notational systems, denoted with an overline.
Don’t Miss: What Does Abiotic Mean In Biology
Theory And Problems Of Boolean Algebra And Switching Circuits
Download Theory And Problems Of Boolean Algebra And Switching Circuits Book For Free in PDF, EPUB. In order to read online Theory And Problems Of Boolean Algebra And Switching Circuits textbook, you need to create a FREE account. Read as many books as you like and Join Over 150.000 Happy Readers. We cannot guarantee that every book is in the library.
Confusing Textbooks? Missed Lectures? Not Enough Time? Fortunately for you, there’s Schaum’s Outlines. More than 40 million students have trusted Schaum’s to help them succeed in the classroom and on exams. Schaum’s is the key to faster learning and higher grades in every subject. Each Outline presents all the essential course information in an easy-to-follow, topic-by-topic format. You also get hundreds of examples, solved problems, and practice exercises to test your skills. This Schaum’s Outline gives you Practice problems with full explanations that reinforce knowledge Coverage of the most up-to-date developments in your course field In-depth review of practices and applications Fully compatible with your classroom text, Schaum’s highlights all the important facts you need to know. Use Schaum’s to shorten your study time-and get your best test scores! Schaum’s Outlines-Problem Solved.
Full Adder And Karnaugh Maps
A useful design tool is the Karnaugh Map developed by Maurice Karnaugh in 1953. This map is another form of truth table that is useful for extracting the math relationships among the input and output values. The table is constructed by listing input values along the top and left axis with the output values in the body of the table. Well use maps to design a full adder with more rigor than used designing the half adder.
A full adder has the same two X and Y inputs but also an input carry, Cin, sent from the previous stage. The outputs are the same, the sum, S, and the output carry, C. For convenience and to eliminate confusion between the two carries well represent Cin by Z in this analysis.
With the truth table defined we can construct two Karnaugh Maps, one for the sum and the other for the carry. The X values run down the left side while across the top are the Y and Z values. Notice that the values for Y and Z are in the order 00, 01, 11, 10 . When multiple inputs are listed the sequence can only change one bit for each column or row. This is called a Gray code.
The body of the map is filled by copying the resultant values for the inputs. For example, in the sum map when X = 1, Y = 0, and Z = 1 the result is 0. The carry result for the same inputs is 1.
Focusing on the sum, the refactoring begins by factoring out X from the first two sub-expressions:
Lets simplify the expression by substituting K for to make the next step more clear.
You May Like: Ccl4 Lewis Structure Shape
Towards Modern Information Technology
- Presents an extensive analysis of the development of switching theory as mathematical foundations for modern logic design, and circuit design in general
- Provides a pictorial history book of Applications of Boolean Logic in Engineering
-
- ebooks can be used on all reading devices
- Immediate eBook download after purchase
- Hardcover 166,39
-
- Free shipping for individuals worldwide
- Institutional customers should get in touch with their account manager
- Usually ready to be dispatched within 3 to 5 business days, if in stock
- The final prices may differ from the prices shown due to specifics of VAT rules
- Softcover 145,78
-
- Free shipping for individuals worldwide
- Institutional customers should get in touch with their account manager
- Usually ready to be dispatched within 3 to 5 business days, if in stock
- The final prices may differ from the prices shown due to specifics of VAT rules
Notes To The Instructor
The project Applications of Boolean Algebra: Claude Shannon and Circuit Design is designed for an introductory or intermediate course in discrete or finite mathematics that considers boolean algebra from either a mathematical or computer science perspective. The project does assume some familiarity with the set operations of union and intersection. This pre-requisite material may be gained by completing the companion project described below, through reading a standard textbook treatment of elementary set operations, or via a short class discussion/lecture. Although no other specific pre-requisite knowledge is necessary for any part of the project, Sections 3 and 4 do assume slightly higher levels of mathematical maturity on the part of the students, roughly commensurate with that of a student who has completed Calculus I and Calculus II .
Implementation with students of any of these projects may be accomplished through individually assigned work, small group work and/or whole class discussion; a combination of these instructional strategies is recommended in order to take advantage of the variety of questions included in the project.
Recommended Reading: Fsa Algebra 1 Eoc Answers
What Is Boolean Algebra
The logical algebra in which symbols represent the logic levels is called Boolean algebra. The logic levels in this algebra are associated with the digits \;and \; for the electronics circuits, logic \ will represent a closed switch, a high voltage, or an on state of a device. Logic \;will represent an open switch or low voltage or off state of the device.
A digital device will either be in any one of these two binary conditions at any given instant. The working of a logic gate can be understood with the help of a light bulb. When logic \ is applied on the switch, it is in an OFF state, and hence the bulb will not glow. When logic \ is applied on the switch, it is in an ON state, and hence the bulb will glow. Logic gates are commonly used in integrated circuits .
Truth Table: A truth table is a tabulated form of the outputs for all possible combinations of inputs that can be applied to a logic gate or circuit. When putting values into a truth table, we often write them as \ or \, where \ represents True, and \ represents False logic.