The Intercept On The Vertical Axis
Figure 21 How to estimate the uncertainty in the gradient.
The other quantity that is normally used to specify the position of a straight line on a graph is its intercept with the vertical axis. We have seen earlier in this module that the equation of a straight line can be written in the form:
y = ax + b
where a is the gradient of the line and b is the intercept with the yaxis that is, the value of y when x = 0.
In the case of the results shown in Figure 20, the intercept is at y = 25m and, since this is determined from the best straight line, we regard it as the best estimate of the intercept.
The maximum and minimum likely values of the intercepts are found by drawing other lines through the error bars, in this case the lines with maximum and minimum slopes shown in Figure 21. The intercepts of these lines are 31m and 22m respectively, and the mean difference between these values and the best intercept is
$\rm = \dfrac\approx 5.0\,m}$
We can, therefore, quote the experimentally determined intercept as m.
Having now determined both gradient and intercept and the possible errors in each we can summarize the experimental results in Figure 20 very succinctly in the form of an equation, namely:
s = ms1×t + m
Question T11
If the errors in the extensions measured in our rubber band experiment are each ±2mm, what is the error in the value of the proportionality constant k?
Figure 31 See Answer T11.
Answer T11
See Figure 31.
Maximum gradient = mmkg1
Thereforek mmkg1.
How To Draw A Line Of Best Fit
To draw the line of best fit, consider the following:
- Outliers must be ignored.
- The line must reflect the trend in the data, i.e. it must line up best with the majority of the data, and less with data points that differ from the majority.
- The line must be balanced, i.e. it should have points above and below the line at both ends of the line.
- DO NOT force the line to pass through any specific data points, or to pass through zero. The purpose of the line of best fit is to reveal the trend of all the data.
Guidelines For Plotting Graphs
Figure 5 Sensible choice of scale. Poor choice of scale.
Figure 6 Readings unevenly spread. Readings evenly spread.
Figure 7 Extra points near to the yaxis.
The last two subsections illustrate how graphs can be useful for exploring the relationship between two variables. This subsection summarizes some important guidelines for plotting graphs of experimental measurements.
1 Plot the independent variable along the horizontal axis and the dependent variable along the vertical axis. For example, to obtain the results shown in Figure 4, various masses were hung from the wire and the resulting extension was measured. The mass is the independent variable and is plotted horizontally, the extension is the dependent variable and is plotted vertically. Figure 4 shows how the extension of the wire depends on the mass hung from it.
2 Label both axes to show what quantity is plotted, and dont forget to include the units. Since only pure numbers can be plotted, the quantity measured must be divided by its units before plotting, which means that the axis should be labelled quantity/units. Thus, in Figure 4, the axes are labelled extension e/mm, and mass m/kg.
5 Plot results clearly. Tiny dots may be confused with dirt on the graph paper, and big dots give loss of precision. Some authors indicate data points with crosses, but dots within circles are more common. i
You May Like: Renate Blauel 2013
Motion With Graphs With Examples
DESCRIBING MOTION WITH GRAPHS
Position vs. Time Graphs:
From the given graph we calculate velocity there is another way of this calculation. We just look at the slope of the graph and find the velocity. What we mean by slope is
which is the equation we use in calculation of the velocity.
2. Position is increasing positive direction.
In this graph our velocity is changing. As a result of this change graph has curved line not linear. So position does not increase linearly. We can also find the velocity of the object from this graph. We should first find the slope of the curve and calculate the velocity.
Example Using the given graph find the velocity of the object in intervals and .
We have seen various type of position vs. time graphs. I think they will help you in solving problems. It is really easy, you should just keep in mind that slope shows the velocity.
Velocity vs. Time Graphs
compare the results of two techniques.
The Intercept Of A Straight Line
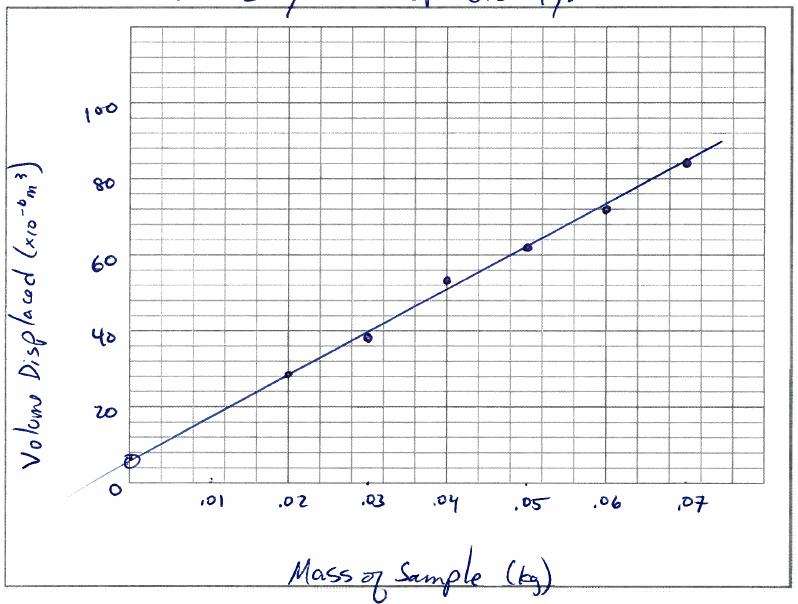
Figure 13 shows the graph of y = 2x + 1. The graph cuts the yaxis at the point y = 1. In other words, when x = 0 the corresponding value of y is 1. The point where the graph cuts the yaxis is called the yintercept, though 2 this is usually abbreviated to intercept.
Find the yintercepts of the lines from the previous question:
y = 3 + 5x y + 2x = 3 5x 2 = 1 2y $3 = \dfrac$
The first step is to rewrite the equation in the appropriate form .
The equation can be rewritten as y = 5x + 3, so yintercept = 3.
The equation can be rewritten as y = 2x + 3, so yintercept = 3.
The equation can be rewritten as $\displaystyle y = \frac + \frac$, so yintercept = 3/2.
The equation can be rewritten as $\displaystyle y = \frac$, so yintercept = 0.
Question T4
From Figure 27, the yintercepts are as follows:
0, 0, 10, 30.
These values correspond to the constants in the equations for the straight lines.
Questions T3 and T4 show that the equations can be written:
y = x +
So the gradient and the yintercept tell us all the characteristics of a straight line, how steep it is and where it lies on the plane in relation to the yaxis. i
We can now refer to a general equation of a straight line:
y = ax + b where a and b are constants
in which the gradient is a and the yintercept is b. i
Find the gradients and intercepts of the straight lines that represent the following linear relationships:
2y + 3 = 2x 2y + x = 6 y 4y + 2 = 6
Recommended Reading: What Does Span Mean Linear Algebra
Whats Asked In A Physics Data Analysis Task
In Physics data analysis task, youll be given a description of the experiment and the experimental data. Then youll be asked to perform quantitative and qualitative analysis.
| Analysis Type | |
|
|
| Qualitative |
|
Determining The Gradient And Intercept Of A Linear Graph
Figure 3 The best straight line drawn through the points.
Figure 4 Extension of a loaded copper wire.
We now return to our rubber band experiment described in Subsection 3.1 and illustrated in Figure 3. Our yvariable here is the extension , and our xvariable is the mass . The line goes through the origin of the graph, so the yintercept is equal to 0. The relationship implied by such a graph is therefore a simple equation relating length and mass:
length = constant × mass
Using symbols to represent the quantities, the equation is more conveniently written as:
e = km
where k represents the constant, usually referred to as the constant of proportionality between e and m.
This is a special case of our general straight line equation, y = ax + b with y = e, x = m, a = k and b = 0.
It is certainly true that we could use the data provided in Table 3 in order to estimate the value of k, but, since we have already plotted this data and fitted a straight line to it in Figure 3, there is a far easier way. The constant k is just the gradient of the line. To determine the gradient we choose two well separated points on the graph, such as the origin and the point , and we use gradient = rise/run, thus
gradient = 105mm/7kg = 15mmkg1
Note that k is expressed in the correct units the units of extension divided by the units of mass .
Having evaluated the constant k we now have an expression relating the two columns of data in Table 3:
e ×m
Question T5
Answer T5
e = ×m
y = x + 7
Also Check: Segment Addition Postulate Color By Number Worksheet Answer Key
Example How Plotting Graph In Physics
Plot the graph of Y= 4, 6, 8, 10, 12 against X= 1, 2, 3, 4, 5
The graph I plotted is shown below
In this graph, i decided to leave six boxes down the graph and six boxes to the left hand side of the graph. This is not a law, it depends on how neat you want your graph to be.
This means I have 18 boxes left for y-axis and 14 boxes left for x-axis. The scale I used was 2cm on the graph represents 2 unit on the y-axis and 2cm on the graph represent 1 unit on the x-axis.
This is how i choose the scale, for y-axis , for x-axis
The next thing is that Located the values on the graph and mark it with a for both y and x axis. Then I joined all the points using a transparent ruler and ensure a line of best fit. The line of best fit is drawn so that the points are evenly distributed on either side of the line.
Note: Make sure you indicate each axis with the symbols you are given with their units. Also indicate your choosen scale at the top of the graph. This information attracts make in physics practical exams.
General note on ploting graphs in physics:
How To Linearize A Curved Data Plot
Adapted from Graphical Methods Summary – Modeling Instruction – AMTA. Also, thanks to Jane Nelson, Orlando, FL, for the memorable naming of graph shapes.
If your data graphs as a curve, the variables you have plotted have a non-linear mathematical form or relationship. Non-linear data is mathematically difficult to analyze. However, if we can convert the data to a linear form we can use our knowledge of straight lines to learn about the physics involved in our experiment. So, if we are confronted with non-linear data then our goal is to convert the data to a linear form that can be easily analyzed. This process is called linearization.
There are four possibilities for graph shapes that we will deal with. Each shape represents data that exhibits a different mathematical form.
| Draw a best fit line and calculate the slope. | Make a new calculated column withthe x-axis variable squared.Then plot y vs. X | Make a new calculated column withthe y-axis variable squared:Then plot Y vs. x | Make a new calculated column withthe x-axis variable as 1/x or 1/x2 . Then plot y vs. X |
LHC & Fermilab Links
Also Check: Books Never Written Pre Algebra With Pizzazz
Reading The Physics In A Graph
Prerequisite
In sciences we often represent a relationship on a graph. We’ve chosen a screwdriver as our icon for reading the physics from a graph since a screwdriver often is what you need to open something up to see what’s inside it that makes it work.
When you learn to create graphs in math classes, you are often showing the graph of a function a relationship between two variables and that’s pretty much the end of it. But in science we graph many functions and many relationships so often we have many different graphs representing the same physical situation.
As a result, graphs can give you multiple views of the same situation. Each graph highlights a different aspect of what’s happening. It’s like picking up a real object and looking at it from different angles, rotating it, turning it over, and looking at it with different lighting.
Looking at a situation using different graphs help make our understanding of what’s happening richer, more coherent, and make more sense.
Blending the reading of graphs with the story tool is particularly useful to see how and what parts of the physical story a graph tells us. Graphs can be valuable tools to help analyze and make sense of a complex situation.
Here are a few hints how to keep your graphing tool sharp and polished:
- Draw your graphs carefully
- Learn to read slopes and areas from a graph
What Are Scientific Graphs
Scientific Graphs are
Straight linear line graphs can also be used to compare changes over the same period of time for more than one group. Pie charts are best to use when you are trying to compare parts of a whole. They do not show changes over time. Bar graphs are used to compare things between different groups or to track changes over time.
Read Also: Ccl4 Dot Structure
Evaluation Of Experimental Method
You must be able to discuss the variables in the experiment and assess the method and the result in terms of:
- Reliability: How close repeated measures are to each other
- Accuracy: How close the final result is to the correct or accepted value.
- Validity: The experimental method and how appropriate it is in addressing the aim of the experiment.
In the evaluation of method and errors part of the data analysis task, youll be also asked to make suggestions for improving the reliability, accuracy and validity of the experiment.
Refer to the table below for assessing the method and the result in terms of validity, reliability and accuracy.
Learn To Read Slopes And Areas From A Graph
In your calculus class, you learn that the derivative of a function is represented by the slope of its graph and that the integral of a function is represented by the area under its graph. In this class we will use slopes and areas on graphs as powerful tools to relate position, velocity, and acceleration or potential energy and force, for example. Check out the follow-ons at the end of this article for details.
Joe Redish 12/27/17
Don’t Miss: How To Calculate Half Life Of A Reaction
Finding The Gradient Of A Straight Line Graph
- The equation of a straight line graph is
- c is the intercept and
- the gradient ‘m’ can be worked out from the change in Y values divided by the change in X values.
Here are the steps to follow when finding the gradient of your graph:
Draw a LARGE triangle, marking the verteces A,B and C and using dashed lines, as shown above. Find what value the sides AC and BC represent by reading off the axes . Write out the equation for the gradient EXACTLY as shown on the diagram above – do NOT miss out steps! Calculate the gradient value Write the value down in the same number of significant figures as it was possible to read from the axes. Add the unit
Overestimation And Underestimation Of Errors
We may expect that the graph is a smooth curve, in which case we would also expect the data points to be scattered around that curve by amounts ranging up to the size of the error bar. For example, in the experiment with the copper wire we can deduce that the errors, or uncertainties, in the experimental measurements must be about ±0.05mm in the extension, and/or ±0.6kg in the mass.
Should the results deviate from a smooth curve by much more than the error bars, as shown in Figure 16, then, either we have underestimated the errors, or the assumption that a smooth curve should describe the results is not valid.
On the other hand, if all the results deviate from the expected curve by much less than the error bars, as in Figure 17, then we might well have overestimated the likely errors.
Figure 16 Have the error bars been underestimated?
Figure 17 Have the error bars been overestimated?
Figure 18 An apparently odd point when gadolinium is heated.
Also Check: Vo In Physics
Evaluation Of Experimental Errors
There are two types of experimental errors: random and systematic error. Experimental errors such as random and systematic errors are always present in an experiment.
In the qualitative part of a Physics data analysis task, youll be asked to
- Identify the type and the source of error.
- Discuss the errors in the experiments and suggest ways of minimising them.
Random and systematics errors are related to reliability and accuracy respectively as illustrated in the flowchart below.