Mental Math Tricks Keep Your Brain Sharp
Yes, those mysterious, new-fangled calculators are beyond helpful. But when you get too reliant on technology, you can just feel things start toslip. Right? It cant just be me. Theres a reason people do Sudoku, puzzles, and crosswords. Mental math tricks are just another brain exercise, and its definitely worth the effort.
Memorize Advanced Multiplication Shortcuts For Specific Problems
Trick : Multiply Any Number By 11
Suppose you want to solve 58 x 11. Can you solve it in less than 5 seconds? Probably you cant. Thats because you dont know one little trick for multiplication by 11. The math trick for multiplying by 11 goes like this:
Imagine a problem like N x 11. Now follow the steps:
Now lets apply the steps with our previous example of 58 x 11:
So, we conclude that 58 x 11 = 638
Don’t Miss: What Is The Molecular Geometry Of Ccl4
Trick : How To Tell The Day For Any Date
Can you tell the day for any date without a calendar at hand? Is that really possible? It is actually a simple skill that anyone can learn. It is also very practical as you may always consider your availability for an activity or an event or you just need to know the day of anyones birthday.
Trick: You may need to memorize some codes to learn this trick, but they are very easy to remember.First, we assign a code number every day of the week.
Second, we assign a code number for every month of the year. These month codes are used for every year with two exceptions. In a leap year, the month code for January is 5 and for February is 1. The month codes with the corresponding mnemonics are as follows:
Third, we assign a code number for every year. For example, the year code for 2011 is 6.
Formula to calculate the day:
Day of the week = mod 7
Note: mod 7 indicates the remainder you get when you divide by 7.
Lets understand this trick with an example:
| Example 1: What is the day of July 16, 2011? |
Day of the week = mod 7
Day of the week = mod 7 = 27 mod 7 = 6
| Example 2: What is the day for December 25, 2011? |
Day of the week = mod 7
Day of the week = mod 7 = 35 mod 7 = 0
Note:It is one of the most useful tricks for competitive exams.
Change The Problem To Make Round Numbers
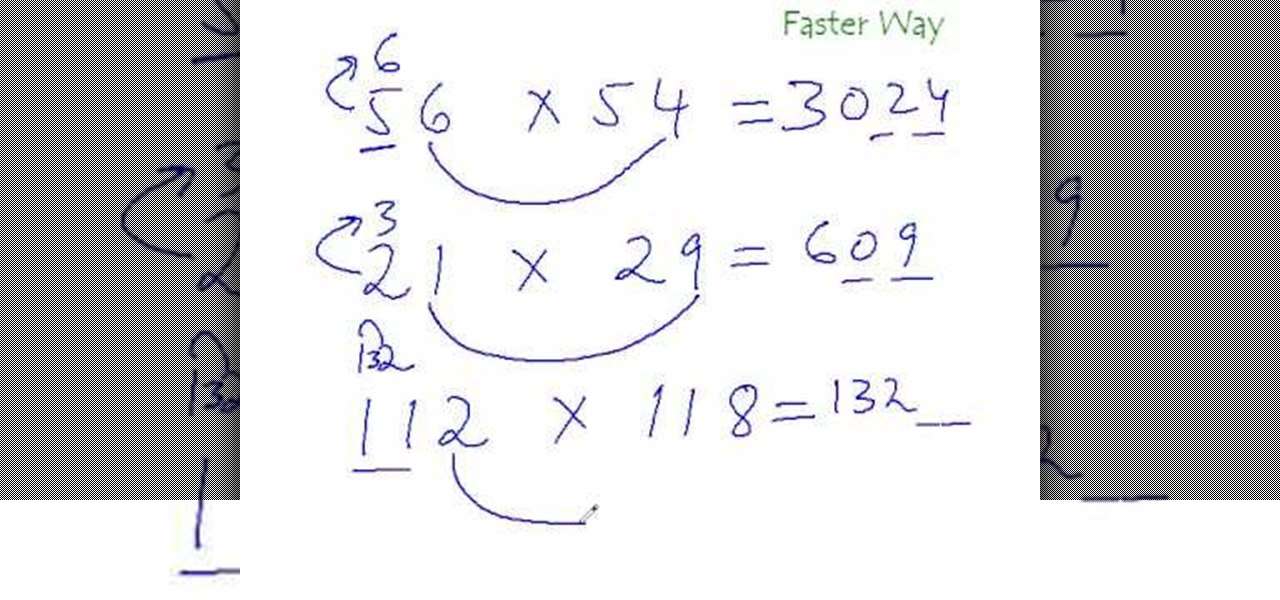
Also Check: Geometry Basics Homework 2 Segment Addition Postulate Answer Key
Of Using A Reference Number
7×8 =
The 10 to the left of the problem is our reference number. It is a number we take our multipliers away from.
Write the reference number to the left of the problem and then ask yourself, are the numbers you are multiplying above or below the reference number? In this case the answer is lower each time. So we put the circles below the multipliers. How much below? 3 and 2. We write 3 and 2 in the circles. Seven is 10 minus 3, so we put a minus sign in front of the 3. Eight is 10 minus 2, so we put a minus sign in front of the 2.
7×8 =
We now work diagonally. Seven minus 2 or 8 minus 3 is 5. We write 5 after the equals sign. Now, multiply the 5 by the reference number, 10. Five times 10 is 50, so write a 0 after the 5. 50 is our subtotal.
Now multiply the numbers in the circles. Three times 2 is 6. Add this to the subtotal of 50 for the final answer of 56.
7×8 = 50
Tip!
If the circled numbers are ABOVE we ADD diagonally, if the numbers are BELOW we SUBTRACT diagonally.
Squaring Numbers That End In Five
This math trick requires two steps, says Snow. In order to square a number that ends in five, take the first digit of the number and multiply it by itself. After, add the result to itself for the answer. For example, if youre multiplying 35 by 35, take the three and multiply it by itself, which is nine, then add three to that answer, which is 12. Finally, add the number 25 to the end of the number you found and that is the final answer: 1,225. Feeling like a math expert? Put your skills to the test and try to pass this math test for fifth graders.
You May Like: Mode In Math Terms
Look At The Last Digit
Look at how the number ends.
If its 0, 2, 4, 5, 6, or 8 you can divide it by 2, 5, or 10.
For example, 28 ends with an even number so its divisible by 2, while 55 ends with a 5 and is divisible by 5.
260 ends with a 0 so its, therefore, divisible by 10.
What about 3 or 9? Add up the digits to find out if the number is divisible by 3 or 9.
A number is divisible by3 if the sum of its digits is equal to a multiple of 3 .
A number is divisible by 9 if the sum of its digits is equal to a multiple of 9 .
If the sum of the digits is divisible by 3 and an even number, its divisible by 6 too.
Simplify Problems With Numbers Ending In Zero
Don’t Miss: How To Calculate Half Lives
How To Calculate Percentage Faster
Finding a percentage of a number is always a tricky process, but if youll think about it in the right terms, youll find that theres a fast percentage finding trick which can save your time. For instance, to find out what 5% of 235 is, follow this method:
- Step 1: Move the decimal point over by one place, 235 becomes 23.5.
- Step 2: Divide 23.5 by the number 2, the answer is 11.75. That is also the answer to the original equation.
Multiplying Numbers Greater Than 10
This method is also working in the case of large numbers.
96 × 97=
What do we take these numbers up to? How many more to make what? 100. So write 4 under 96 and 3 under 97.
96 × 97=
Then subtract diagonally. 96-3 or 97-4 is 93. This is the first part of your answer. Now, multiply the numbers in the circles. 4 × 3=12. This is the last part of the answer. The finished answer is 9,312.
96 × 97=9,312
This method is certainly easier than the method you learned in school! We believe that everything genial is simple, and maintaining simplicity is a hard work.
Recommended Reading: How To Calculate Half Life Chemistry
Find Percent Or Any Big Number In A Minute
This one is the easiest of all and our personal favorite among all the Maths Tricks we have learned till now. The reason: We have seen so many students struggling with squaring large numbers and taking more than 10 minutes in doing so, which is illogical. But, they dont know the Maths Tricks so ten minutes are not a big deal for them. The pen and pencil method is the only way they know.
We have a better way. From now on, lets find a percentage our way:
Lets say, we have to find 10% of 45609. Such a big number, no? but what if we say that you have to only divide the number by 10?
Step1 : Divide the number by 10. You get your answer: 4560.9
Now, if you have to find 20% of the same number.
Step 1: Multiply the 10% of the number by 2. The answer: 9121.8
Same in the case of 30%
Step 1: Multiply the 10% of the number by 2. Your answer is: 13682.7
So on, and so forth. Practice these Maths Tricks with your siblings and surprise them with your superpowers. For better understanding, you can always take the help of our videos.
Our Suggestion
Now, as you know so many tricks, the real challenge is to bring them into practice. Initially, you will find the conventional method more comfortable. But, you have to get out of your comfort zone to ace these tricks and techniques. We can bet within a few days, you will start doing all your mathematics calculations with the help of these Maths Tricks only.
What Is A Multiplicand And A Multiplier
Before we get into multiplication tricks to do mental math, let us quickly define what a multiplicand and a multiplier is. Take for example, the multiplication problem 43 x 23. Here the number 43 is the multiplicand the number being multiplied. The number 23 is the multiplier the number which is multiplying the first number.
There are several multiplication tricks for mental math in this post. Each mental multiplication method will have two examples. The first example, visible to everybody, will introduce you to the multiplication trick. The second example, visible only to logged-in users, will have variations not covered in the first example. So log in or to access the entire content.
You May Like: Half Life Calculation Formula
Divide A Large Number By 5
These Vedic Maths Tricks are by far the easiest of all the tricks mentioned here. Yes, you can divide any large or small numbers with 5 in a jiffy. Hey! Wait. We are not just talking about numbers ending with 5. But, other numbers as well. Actually, any number with any number of digits.
Lets divide 67834 by 5
Step 1: Multiply the number by 2.
= 67834 × 2 = 135668
Step 2: Move a decimal point to the left.
= 13566.8
The left side of the decimal point is your answer. Oh! Yes. Just in two steps. You got your answer: 13566.
We dare you to try the same Maths Trick with larger numbers and do let us know, how it worked for you.
Recap: What Are Percentages
To make sure were all on the same page, lets kick things off by taking a minute to recap a few key facts about percentages. Lets start with the most important question: What are percentages? Perhaps the most illuminating thing to know is that the word percent is really just the phrase per cent squashed together. And since cent here means 100 , we see that the word percent just means per 100. In other words, 10% means 10 per 100, which is the same as the fraction 10/100 or 1/10.
This turns out to be great news since it makes lots of percentages easy to calculate. In particular, its easy to calculate 10% of any number since thats just 1/10 of the number. Why is that so helpful? Because it means that you can quickly calculate 10% of a number simply by moving its decimal point 1 position to the left.
But what about calculating something like 36% of 25? Or maybe 250% of 20? In these cases, our trick of using the power of 10% doesnt helpso what can we do?
Also Check: Kim Kardashian’s Biological Father
Online Resources To Improve Your Mental Arithmetic
The internet is an excellent resource to help you improve your math skills. There are plenty of websites that have more than one lesson with quizzes, tests, and exercises.
- BBC Bitesize: The BBC provides resources for students of all ages. Great school-aged children.
- Khan Academy: This website features video lessons as well as practice questions to help you learn.
If you want to get good at math and mental arithmetic you need to learn the basic principles by heart as much as you know the addition and multiplication tables.
Train your brain to remember, everything will become second nature, and your ability in mental arithmetic will increase exponentially.
This, of course, requires time and a personal commitment but the result is worth the cost because youll have these reflexes for the rest of your life.
How To Do It
Heres an example: Lets say you need to add the numbers 1, 3, 5, 7, and 9. You could run through the numbers in order, adding them up one-by-one something like:
1 + 3 = 4, then9 + 7 = 16, and finally16 + 9 = 25.
But thats a lot to keep track of. Remember the commutative property of addition? You don’t have to add these numbers in the order they’re given to you. Instead, if you start by pairing up numbers that add to tenin this case 3 and 7, and 9 and 1that leaves you with an easy problem. You just have to add the two 10s to the remaining number 5 that didnt pair with anything: 10 + 10 + 5 = 25
You May Like: Who Is Paris Jackson Mom
Maths Short Tricks For Tough Multiplication
When multiplying large numbers, if one of the numbers is even, divide the first number in half, and then double the second number. This method will solve the problem quickly. For instance, consider
20 x 120
Step 1: Divide the 20 by 2, which equals 10. Double 120, which equals 240.
Then multiply your two answers together.
10 x 240 = 2400
The answer to 20 x 120 is 2,400.
Multiplying Using Two Reference Numbers
Previous method for multiplication has worked well for numbers that are close to each other. When the numbers are not close, the method still works but the calculation become more difficult.
It’s possible to multiply two numbers that are not close to each other by using two reference numbers.
8 × 27=
Eight is close to 10, so we will use 10 as our first reference number. 27 is close to 30, so we use 30 as our second reference number. From the two reference numbers, we choose the easiest number to multiply by. It is 10. This becomes our base reference number. The second reference number must be a multiple of the base reference number. 30 is 3 times the base reference number 10. Instead of using a circle, write the two reference numbers to the left of the problem in brackets.
8 × 27=
Both the numbers in the example are lower than their reference numbers, so draw the circles below.
How much are 8 and 27 lower than their reference numbers ? 2 and 3. Write these numbers in the circles.
8 × 27=
Now multiplythe2 below the 8 by the multiplication factor 3 in the parentheses.
2 × 3=6
Write 6 in the bottom circle below the 2. Then take this bottom circled number 6, diagonally away from 27.
27-6=21
Multiply 21 by the base reference number 10.
21 × 10=210
210 is our subtotal. To get the last part of the answer, multiply two numbers in the top circles, 2 and 3, to get 6. Add 6 to our subtotal of 210 and get our finished answer of 216.
Creative Commons
Don’t Miss: Holt Mcdougal Geometry Chapter 7 Test