X 4 + X3 3×3 + 6 X 2 + 4 X + 1 3x 3 + 3x 2 3x 2 + 4 X + 1 3x 2 + 3x X +1 Nuevo Dividendo
ww w.
3x 2 + 4 x + 1
3×3 + 6 x 2 + 4 x + 1
x 4 + x3
ic a1
Nuevo dividendo 3×3 + 6 x 2 + 4 x + 1 La diferencia encontrada entre el dividendo y el producto mencionado resulta ser el nuevo dividendo. Se repite el proceso anterior, las veces que resulte necesario, hasta que el grado del polinomio que aparece como nuevo dividendo sea menor que el grado del polinomio que est en el divisor, como se muestra enseguida: x3 + 3x 2 4 3 x + 1 x + 4 x + 6 x 2 + 4 x +1.c o m
x3 + 3x 2 + 3x + 1 x + 1 x 4 + 4 x 3 + 6 x 2 + 4 x +1 x 4 + x3 3×3 + 6 x 2 + 4 x + 1 3x 3 + 3x 2 3x 2 + 4 x + 1 3x 2 + 3x x +1 x +1 0 Se termina el proceso El resultado anterior significa que la divisin es exacta y que el dividendo se puede escribir en la forma: x 4 + 4 x 3 + 6 x 2 + 4 x + 1 =
ww w.
iii)
x4 + 4 x3 + 6 x 2 + 4 x + 1 x2 + 2x + 1 iv) x 2 + 2 x + 1 x 4 + 4 x 3 + 6 x 2 + 4 x + 1
ic a1
e) Dividiremos el polinomio de cuarto grado x 4 + 4 x 3 + 6 x 2 + 4 x + 1 entre el trinomio de segundo grado x 2 + 2 x + 1 . Algunas de las formas en que podemos denotar la divisin mencionada son: i) ii) /.c o m
x2 + 2x x 2 + 2 x + 1 x 4 + 4 x 3 + 6 x 2 + 4 x +1 x 4 + 2 x3 + x 2 2 x3 + 5 x 2 + 4 x + 1 2 x3 + 4 x 2 + 2 x x2 + 2x + 1 x2 + 2x + 1 x + 2 x + 1 x + 4 x + 6 x 2 + 4 x +12 4 3
Nuevo dividendo
ww w.
ii) /
f) Dividiremos el polinomio de cuarto grado x 4 + 4 x 3 + 6 x 2 + 4 x + 1 entre el polinomio de tercer grado x 3 + 3 x 2 + 1 . Algunas de las formas en que podemos denotar la divisin mencionada son: i)
Qu Es Un Trmino Algebraico
En esta página aprenderás, qué es un término algebraico y también a definir el grado y, grado absoluto del mismo. Encontraras ejemplos y ejercicios para practicar.
En álgebra, un término algebraico, es un solo número o variable, o números y variables multiplicados entre sí. Los términos están separados por los signos + o . Ejemplo:
Ejemplo Resuelto De Una Ecuacin
Para ver a fondo el proceso de resolución de una ecuación,vamos a plantear la siguiente:
4x + 10 = 25 x
Para resolver esta ecuación debemos despejar la incógnita. Para ello, en primer lugar, se procede a agrupar los términos semejantes. Básicamente, esta parte consiste en pasar todas las incógnitas al lado izquierdo y todas las constantes al lado derecho.
Así tenemos.
Sumando y restando estos términos semejantes, tenemos.
5x = 10
Finalmente, se procede ahora a despegar la incógnita ydeterminar su valor.
x = 10/5
Read Also: Different Types Of Lines In Geometry
Clases De Trminos Algebraicos
Por otro lado, el Álgebra también se ha dado a la tarea de desarrollar una clasificación de términos algebraicos, hecha según las semejanzas, diferencias o ausencias de su elementos literal, el cual es el que finalmente, determinará a qué clase pertenece un término algebraico específico. En este sentido, se puede considerar que básicamente existen tres tipos de términos algebraicos, los cuales se describen seguidamente:
Ejemplos De Suma Y Resta De Trminos Algebraicos

Para demostrarte el poder matemático de la reducción de términos semejantes, a continuación te mostraremos un par de ejemplos:
Primero, conviene separar cada literal, operando a sus términos semejantes de la siguiente manera:
Y por último, sumamos a los coeficientes:
Resultando el polinomio:
Resultando:
Read Also: Who Was The Founder Of Behaviorism
X 4 + 3×3 + 0 X 2 + X X 3 + 6 X 2 + 3x + 1 X3 + 3x 2 + 0 X + 1 3x 2 + 3x Se Termina El Proceso
El resultado anterior significa que la divisin no es exacta y que el dividendo se puede escribir en la forma: x 4 + 4 x 3 + 6 x 2 + 4 x + 1 = + 3 x 2 + 3 x
g) Dividiremos el polinomio de tercer grado x 3 y 3 entre el binomio de primer grado x y . Algunas de las formas en que podemos denotar la divisin mencionada son: i) ii) /.c o
iii)
iv) x y x 3 y 3
Utilizando, ahora si, la notacin iv), se divide el primer trmino del dividendo entre el primer trmino del divisor y el cociente se multiplica por los trminos del divisor escribiendo el producto debajo del dividendo, tratando de que queden las mismas potencias alineadas, restndose a continuacin dicho producto del dividendo, segn se muestra en seguida: x2 x y x3 + 0 x 2 + 0 x y 3 x3 x 2 y x2 y + 0x y3 Nuevo dividendo
La diferencia encontrada entre el dividendo y el producto mencionado resulta ser el nuevo dividendo. Se repite el proceso anterior, las veces que resulte necesario, respecto a la variable principal considerada, hasta que el grado del polinomio que aparece como nuevo dividendo sea menor que el grado del polinomio que est en el divisor, como se muestra a continuacin:
ww w.
Primero observamos que en el dividendo aparece dos trminos, x3 y y3, si tomamos como variable principal del polinomio a la letra x, entonces debemos escribir el binomio como un polinomio completo de tercer grado agregando ceros y considerando el trmino y3 como su trmino independiente, segn se muestra a continuacin: x y x3 + 0 x 2 + 0 x y 3
ii) /
Ejemplos De Funciones Algebraicas
Existen al menos 30 tipos de funciones algebraicas, pero entre las más destacadas, se tienen los siguientes ejemplos:
1. Función explícita: =sen
2. Función implícita: yx=9×3+x-5
3. Función polinómica:
b) Primer grado o lineal: =3+4
c) Segundo grado o cuadrática: = 2+2+1 ó 2
d) Tercer grado o cúbica: =2 3+4 2+3 +9
4. Función racional:
7. Función por secciones: =si 0 5
Also Check: What Is Relationship In Math
A Qu Se Debi La Fama De Este Libro
Su éxito radica en que es, además de una famosa obra literaria obligatoria en las secundarias de Latinoamérica, el libro más consultado y completo sobre la materia, por contener una explicación clara sobre los conceptos y sus ecuaciones algebraicas, así como datos históricos sobre los aspectos a estudiar, en el que se maneja el lenguaje algebraico.
Este libro es la iniciación por excelencia para los estudiantes dentro del mundo algebraico, aun cuando para algunos representa una fuente de estudios de inspiración y para otros sea temido,lo cierto es que es una bibliografía obligatoria e ideal para la mejor comprensión de los temas abarcados.
Qu Es Literal Y No Literal
Vamos a ver cuál es la diferencia entre literal:Se ha denominado su diferencia entre literal y no literal, ya que su significado estándary, en contraposición, significado no literal, es decir, a este otro significado no coincidente con el anterior.
Es por eso que se expresan significados no literales mediante diversas figuras literarias .
Recommended Reading: Hawkes Learning Systems Statistics Answer Key
Qu Es El Lgebra De Baldor
Cuando se habla de qué es el álgebra de Baldor, se refiere a una obra desarrollada por el matemático, profesor, escritor y abogado Aurelio Baldor , la cual fue publicada en el año 1941. En la publicación del profesor, quien nació en La Habana, Cuba, se reseñan 5.790 ejercicios equivalentes a un promedio de 19 ejercicios por prueba.
Baldor publicó otras obras, tales como Geometría plana y del espacio, Trigonometría de Baldor y Aritmética de Baldor, pero la que más ha tenido impacto en el ámbito de esta rama ha sido el Álgebra de Baldor.
Este material, sin embargo, es más recomendado para el nivel educativo medio , ya que para niveles superiores apenas serviría como complemento para otros textos más avanzados y acordes a dicho nivel.
La famosa portada en la que aparece el matemático, astrónomo y geógrafo persa musulmán Al-Juarismi , ha representado confusión entre los estudiantes que se han servido de esta famosa herramienta matemática, ya que se piensa que este personaje se trata de su autor Baldor.
El contenido de la obra se encuentra dividido en 39 capítulos y un apéndice, el cual contiene tablas de cálculos, cuadro de formas básicas de descomposición de factores y tablas de raíces y potencias y al final del texto se encuentran las respuestas de los ejercicios.
Es Del Trmino Algebraico
Tomando en cuenta la definición de Término algebraico se puede concluir entonces que este será todo elemento conformado por una combinación de letras y números en donde no existen signos matemáticos de suma o resta. Por ende, se pueden considerar como términos algebraicos aquellos que se muestran a continuación:
ab3 -2xy23ab
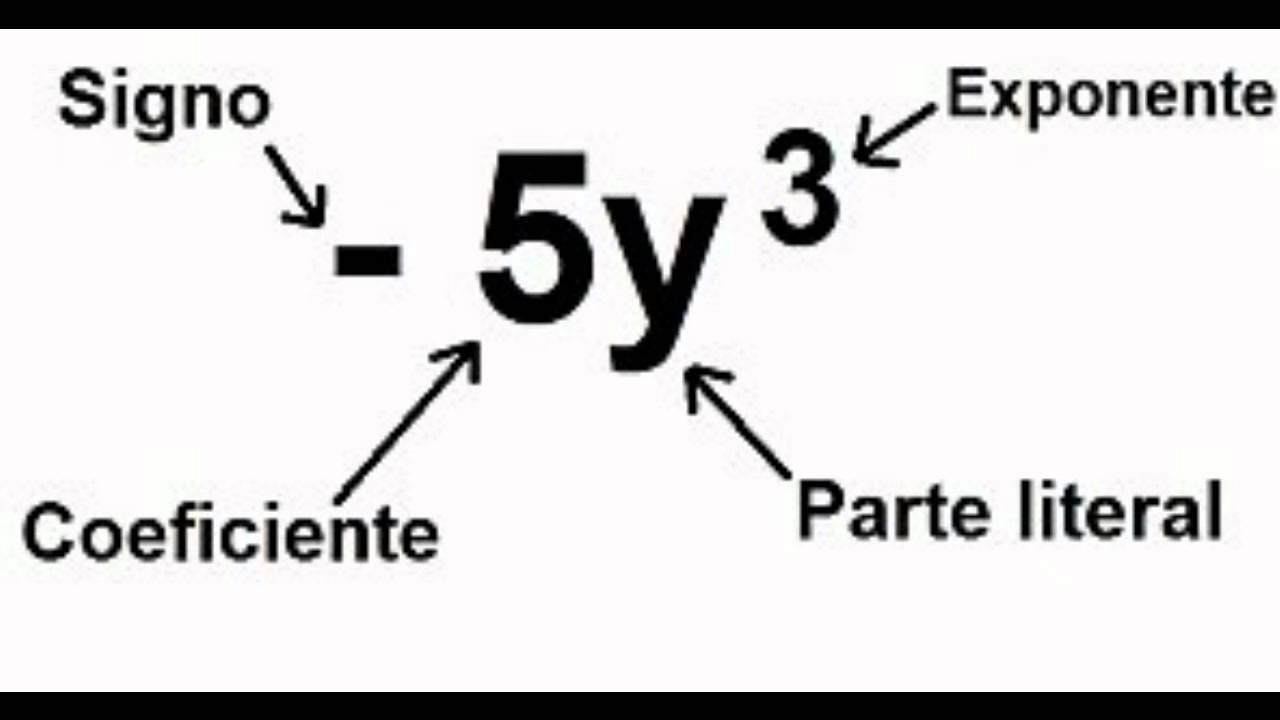
Sin embargo, como puede verse el término algebraico se encuentra compuesto a su vez por varios elementos, tanto de tipo numérico como no-numérico, los cuales conformarían las distintas partes del término algebraico, y que se pueden identificar tal como se muestra a continuación:
De tal manera, todo término algebraico estará conformado por cuatro elementos, sin que sea necesario que todos estén presentes de forma continua, para que la expresión pueda ser considerada un término algebraico, puesto que pueden existir términos que no tengan presencia de exponente, de coeficiente o de parte literal, sin que esto indique que no sea un término algebraico. En cuanto al signo, por convenciones matemáticas, cuando no es expresado de forma explícita, se asume que responde al signo cuya función no es indicar suma sino que viene a señalar si el elemento que acompaña es de naturaleza positiva o negativa. No obstante, resulta pertinente también, revisar las definiciones de cada uno de los cuatro elementos que conforman el término algebraico:
Don’t Miss: Algebra 1 Week 1 Fsa Countdown Answers
Trminos Algebraicos No Semejantes
En contraparte, cuando se esté frente a dos o más signos algebraicos en donde no exista coincidencia entre los literales por los que están conformados, se hablará entonces de términos algebraicos no semejantes, como por ejemplo, los que se muestran a continuación:
4ab25y32xy
son tres términos donde no existe coincidencia en cuanto a su literal, por lo que son tomados como términos algebraicos no semejantes.
Tipos De Literal Y Sus Definiciones
Que es literal, en la transcripción de un texto o nota, la escritura alfabética a otra lengua, solemos decir procedió a una transcripción literal, es decir, cuanta una de esta palabra se haya ejecutado mediante una letra por letra.
Te puedes interesar:
Ejemplo de literal unas bonitas palabras literales es la cualidad de la vida,da entender su contexto y su compresión al que la escucha. A continuación, vamos a ver los tipos de literal.
Don’t Miss: My.hrw Answer Key
Qu Significa Literal En Espaol
Si deseas saber cuál es la definición de literal, aquí en este artículo vamos a definírtelos. Literal se refiere a un adjetivo el cual es empleado para hacer referencia a aquella interpretación que mayormente se utilizan en el escrito,nota, apunte o documentoy se origina de las palabras plasmadas en él.
El origen de la palabra literal proviene del latín, que significa litterlis, dicho de otro término, es relativo a la letra, y deben entender que este vocablo no se debe confundirse con literario.
- La expresión de literalhace referencias a ciertos términos:
- Se refiere a lo relativo a la letra .
- Cuando se está leyendo un texto o produce al pie de la letra .
- Lenguaje literalpor contrariedad del lenguaje figurado: símiles, analogía, metáfora, etc.
- Traducción literal: La conexión del riguroso de una traducción a las formas de un texto.
- Interpretación literal
- Liberalismo en música:es un método que se utilizan para componer música.
- Objeto literal, string literalo función literal los tipos de alfabetos que representan y dan valor al lenguaje de programación de código fuente.
- Revista litera.
En relación con eso, el concepto de Literal y Literariopertenece todo aquello que venera o respeta fielmente el sentido propio de las palabras de otros. Por esta razón es que se contrapone con el sentido figurado a lato, dicho de otra forma, se utilizan para atribuir o se deduce de las palabras.
Qu Suelen Representar Los Literales
Los números literales son las letras que se utilizan para representar un número. Los números literales obedecen todas las reglas de adición, sustracción, multiplicación y división de números. Así, a + b significa que b se suma a aa b significa que b se resta de aa × b significa que a se multiplica por ba ÷ b significa que a se divide por bNota: En la multiplicación, a veces se utiliza el punto . en lugar de ×. El signo . o × generalmente se omite entre un dígito y una letra o entre dos o más letras.Por ejemplo: 5 × a o 5a puede escribirse como 5a. 10 × p puede escribirse como 10p o 10p. a × b puede escribirse como ab o ab. 2 × a × b puede escribirse como 2ab o 2ab. a × b × c puede escribirse como abc o abc. x × y × z puede escribirse como xyz o xyz. 5 × l × m × n puede escribirse como 5lm.n o 5lmn. a × x × y × z puede escribirse como axy.z o axyz. 10 × j × k × l × m puede escribirse como 10.j.k.l.m o 10jklm. 1000 × x puede escribirse como 1000.x o 1000x.Pero nunca debe omitirse . o × entre los dígitos.
Also Check: College Algebra 2nd Edition Julie Miller Ebook
Estas Son Las Principales Expresiones Algebraicas
Existen expresiones que forman parte del concepto de qué es el álgebra, dichas expresiones se clasifican en dos tipos: los monomios, que son los que tienen un único sumando y los polinomios, que tiene dos , tres o más sumandos.
Publicidad
Algunos ejemplos de monomios serían: 3x, .
Mientras que algunos polinomios pueden ser: 4×2+2x 7ab+3a3.
Es importante mencionar que si la variable se encuentra en el denominador o dentro de una raíz, las expresiones no serían ni monomios ni polinomios.
Definicin De Trmino Algebraico
En ese sentido, se puede comenzar entonces por recordar de forma breve la definición de Término algebraico, el cual es concebido por el Álgebra como la expresión algebraica más elemental, constituida por una combinación de elementos abstractos numéricos y no numéricos . Así mismo, como rasgo esencial del término algebraico se encuentra la no cabida de operaciones de suma, resta y división entre estos números y letras, permitiéndose entonces únicamente las operaciones de multiplicación planteadas entre el coeficiente y el literal, al igual que las operaciones de potenciación que tienen lugar entre el literal y su exponente.
Recommended Reading: What Does Abiotic
X B Realizaremos La Siguiente Operacin 4 X4 X = 4 4 4 4 4 X X = 4 4 256 Por Lo Tanto
b = 2 a
a) Escribiremos una expresin equivalente a a 2b exponentes positivos. De las leyes de los exponentes, se tiene que:
ic a1(
Una de las aplicaciones ms importantes de las leyes de los exponentes y de la factorizacin es en la simplificacin de expresiones algebraicas donde aparecen fracciones.
Qu Es El Lgebra Lineal
Esta área de la matemática y del álgebra, es la que estudia los conceptos de vectores, matrices, sistemas de ecuaciones lineales, espacios vectoriales, transformaciones lineales y las matrices. Como se puede observar, tiene diversas aplicaciones el álgebra lineal.
Su utilidad varía desde el estudio del espacio de las funciones, que son aquellas que se definen por un conjunto X a un conjunto Y y se aplican para espacios vectoriales o topológicos las ecuaciones diferenciales, las cuales relacionan a una función con sus derivadas la investigación de operaciones, que aplica métodos analíticos avanzados para tomar decisiones acertadas hasta la ingeniería.
Uno de los ejes principales del estudio del álgebra lineal se encuentra en los espacios vectoriales, que son conformados por un conjunto de vectores y un conjunto de escalares .
Los principales espacios vectoriales de dimensión finita, son tres:
- Los vectores en Rn, que representan coordenadas cartesianas .
- Las matrices, que son sistemas rectangulares de expresiones , se caracterizan por una cantidad de filas y una cantidad de columnas , y se usan en ciencias y la ingeniería.
- El espacio vectorial de polinomios en una misma variable, dado por polinomios que no superan el grado 2, poseen coeficientes reales y se encuentran sobre la variable x.
Read Also: The First Pioneer Species To Appear In An Area Undergoing Secondary Succession Is
Diferencia Entre Literales Y Variables En Lgebra
A veces nos dan una fórmula, por ejemplo de geometría, y necesitamos resolver para alguna variable distinta de la «estándar». Por ejemplo, la fórmula del perímetro P de un cuadrado con lados de longitud s es P = 4s. Es posible que necesitemos resolver esta ecuación para s porque tenemos muchos perímetros de cuadrados y queremos introducir esos valores de perímetro en una fórmula y que esa fórmula arroje el valor de la longitud de cada lado del cuadrado. Este proceso de resolver una fórmula para una variable específica se llama «resolver ecuaciones literales».Una de las definiciones del diccionario de «literal» es «relacionado con o compuesto por letras», y las variables se denominan a veces literales. Así que «resolver ecuaciones literales» parece ser otra forma de decir «tomar una ecuación con muchas letras, y resolver para una letra en particular».A primera vista, estos ejercicios parecen ser mucho peores que nuestros ejercicios de resolución habituales, pero en realidad no son tan malos. Hacemos más o menos lo mismo que hemos hecho todo el tiempo para resolver ecuaciones lineales y otros tipos de ecuaciones la única diferencia sustancial es que, debido a todas las variables, no podremos simplificar nuestro trabajo a medida que avanzamos, ni tanto como estamos acostumbrados al final. Así es como funciona la resolución de ecuaciones literales:
Relacionados