Sequences And Series Cumulative Assessment
Question 1.The frequencies of the notes on a piano form a geometric sequence. The frequencies of G and A are shown in the diagram. What is the approximate frequency of E at ?Answer:
Question 2.You take out a loan for $16,000 with an interest rate of 0.75% per month. At the end of each month, you make a payment of $300.a. Write a recursive rule for the balance an of the loan at the beginning of the nth month.b. How much do you owe at the beginning of the 18th month?c. How long will it take to pay off the loan?d. If you pay $350 instead of $300 each month, how long will it take to pay off the loan? How much money will you save? Explain.Answer:
Question 3.The table shows that the force F needed to loosen a certain bolt with a wrench depends on the length of the wrenchs handle. Write an equation that relates and F. Describe the relationship.Answer:
Question 4.Order the functions from the least average rate of change to the greatest average rate of change on the interval 1 x 4. Justify your answers.Answer:
Question 6.The diagram shows the bounce heights of a basketball and a baseball dropped from a height of 10 feet. On each bounce, the basketball bounces to 36% of its previous height, and the baseball bounces to 30% of its previous height. About how much greater is the total distance traveled by the basketball than the total distance traveled by the baseball?A. 1.34 feet
Arithmetic Sequences And Series
An arithmetic sequence is a sequence of numbers such that the difference of any two successive members of the sequence is a constant.
Example
2,4,6,8,10.is an arithmetic sequence with the common difference 2.
If the first term of an arithmetic sequence is a1 and the common difference is d, then the nth term of the sequence is given by:
$$a_=a_+d$$
An arithmetic series is the sum of an arithmetic sequence. We find the sum by adding the first, a1 and last term, an, divide by 2 in order to get the mean of the two values and then multiply by the number of values, n:
$$S_=\frac$$
Example
Find the sum of the following arithmetic series 1,2,3..99,100
We have a total of 100 values, hence n=100. Our first value is 1 and our last is 100. We plug these values into our formula and get:
$$S_=\frac=5050$$
Get Algebra 2 Sequences And Series Worksheet From Our Site
Furthermore, you will find an algebra software instrument that helps you fix some difficult algebra equations which algebra calculator is the perfect solution you are searching for. These calculators can help you when you, when you find yourself stuck on the problem and not capable to obtain the respond to. These web based calculators will give you some will give you details as well as a comprehensive explanation from the problem in one step-by-move procedure. You can find a wide range of calculators in the online, which can be utilizing different methods to solve these complications. And some of the calculator software program can help you in making use of various other strategies, which help you in fixing algebra queries. And in addition, you can find a few other graphing calculators who plot queries. This type of calculators will allow you to fix graphical Algebra 2 Sequences And Series Worksheet questions.
Besides this, you can get a few other supplemental tool in the internet will be the well-known algebra solver. When when compared with calculator, the performance is identical and also this software package can provide answers for most difficult concerns also. All that you need to get in the situation, and also the computer software will do all of those other points. This software program will provide an internet instructor whenever your youngsters need, and it will save large cash on working with a tutor.
Don’t Miss: Does Michael Jackson Have Any Biological Kids
Chapter : Series And Sequences
In this chapter well be taking a look at sequences and series. In fact, this chapter will deal almost exclusively with series. However, we also need to understand some of the basics of sequences in order to properly deal with series. We will therefore, spend a little time on sequences as well.
Series is one of those topics that many students dont find all that useful. To be honest, many students will never see series outside of their calculus class. However, series do play an important role in the field of ordinary differential equations and without series large portions of the field of partial differential equations would not be possible.
In other words, series is an important topic even if you wont ever see any of the applications. Most of the applications are beyond the scope of most Calculus courses and tend to occur in classes that many students dont take. So, as you go through this material keep in mind that these do have applications even if we wont really be covering many of them in this class.
Here is a list of topics in this chapter.
Sequences In this section we define just what we mean by sequence in a math class and give the basic notation we will use with them. We will focus on the basic terminology, limits of sequences and convergence of sequences in this section. We will also give many of the basic facts and properties well need as we work with sequences.
Lesson 83 Analyzing Geometric Sequences And Series
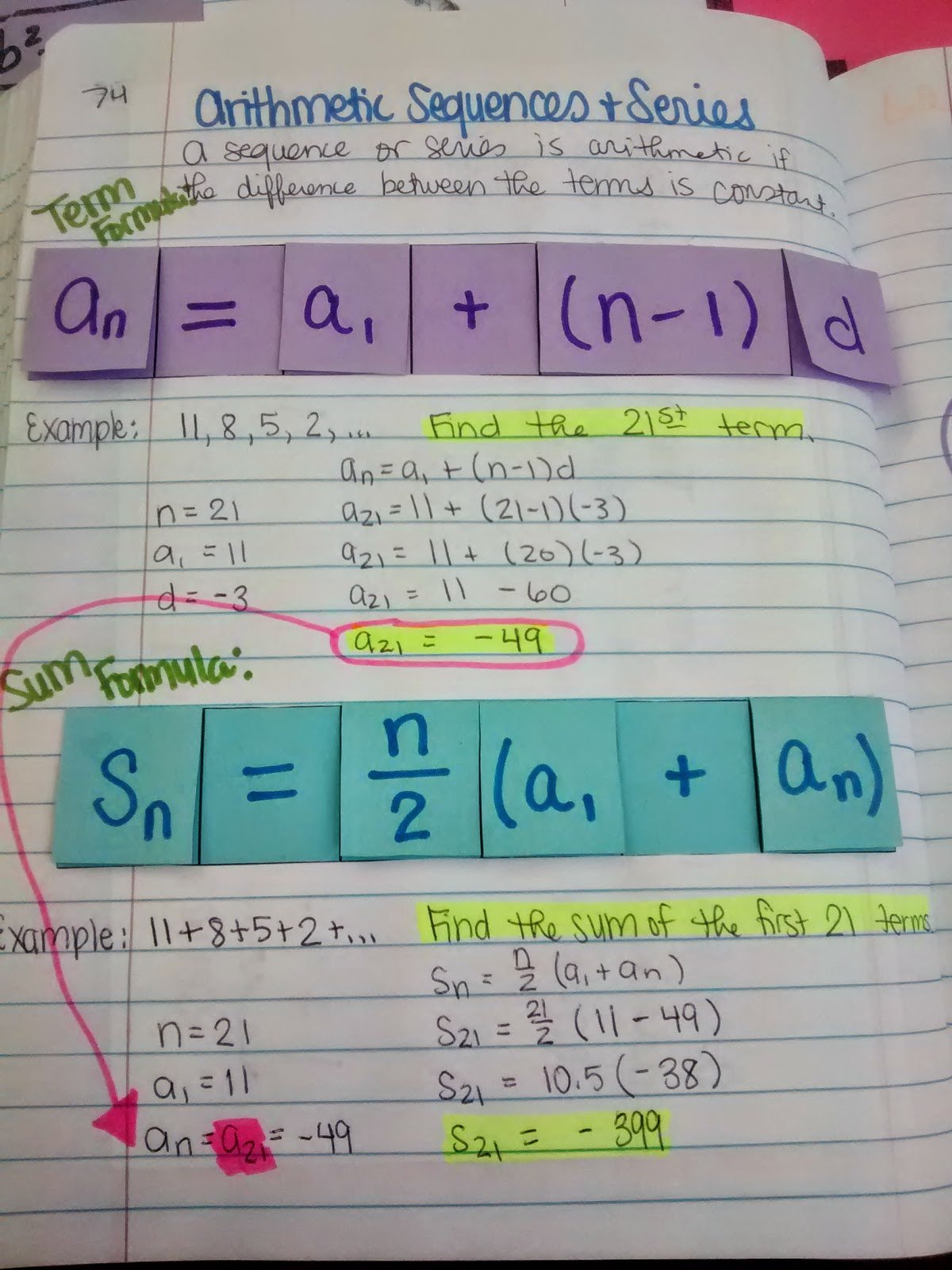
Essential Question How can you recognize a geometric sequence from its graph?In a geometric sequence, the ratio of any term to the previous term, called the common ratio, is constant. For example, in the geometric sequence 1, 2, 4, 8, . . . , the common ratio is 2.
EXPLORATION 1
Recognizing Graphs of Geometric SequencesWork with a partner. Determine whether each graph shows a geometric sequence. If it does, then write a rule for the nth term of the sequence and use a spreadsheet to find the sum of the first 20 terms. What do you notice about the graph of a geometric sequence?
EXPLORATION 2
Finding the Sum of a Geometric SequenceWork with a partner. You can write the nth term of a geometric sequence with first term a1 and common ratio r asan = a1rn-1.So, you can write the sum Sn of the first n terms of a geometric sequence asSn = a1 + a1r + a1r2 + a1r3 + . . . +a1rn-1.Rewrite this formula by finding the difference Sn rSn and solve for Sn. Then verify your rewritten formula by funding the sums of the first 20 terms of the geometric sequences inExploration 1. Compare your answers to those you obtained using a spreadsheet.
Communicate Your Answer
How can you recognize a geometric sequence from its graph?Answer:
Find the sum of the terms of each geometric sequence.a. 1, 2, 4, 8, . . . , 8192b. 0.1, 0.01, 0.001, 0.0001, . . . , 10-10Answer:
Tell whether the sequence is geometric. Explain your reasoning.Question 1.27, 9, 3, 1, \, . . .Answer:
2, 6, 24, 120, 720, . . .Answer:
You May Like: Mcgraw Hill Geometry Answers
Big Ideas Math Algebra 2 Answers Chapter 8 Sequences And Series
Big Ideas Math Algebra 2 Answer Key Chapter 8 Sequences and Series helps you to get a grip on the concepts from surface level to a deep level. Finish your homework or assignments in time by solving questions from B ig Ideas Math Book Algebra 2 Ch 8 Sequences and Series here. Access the user-friendly solutions provided for all the concepts of Chapter 8 Sequences and Series from Big Ideas Math Algebra 2 Textbooks here for free of cost.
Improve your performance in the final exams by practicing the Big Ideas Math Algebra 2 Answers Ch 8 Sequences and Series on a daily basis. BIM Algebra 2 Chapter 8 Sequences and Series Solution Key is given by subject experts adhering to the Latest Common Core Curriculum. Sequences and Series Big Ideas Math Algebra 2 Chapter 8 Answer Key encourages students and teachers to learn math in a simple and fun learning way.
Sequences And Series Mathematical Practices
Mathematically proficient students consider the available tools when solving a mathematical problem.
Monitoring Progress
Use a spreadsheet to help you answer the question.Question 1.A pilot flies a plane at a speed of 500 miles per hour for 4 hours. Find the total distance flown at 30-minute intervals. Describe the pattern.Answer:
Question 2.A population of 60 rabbits increases by 25% each year for 8 years. Find the population at the end of each year. Describe the type of growth.Answer:
Question 3.An endangered population has 500 members. The population declines by 10% each decade for 80 years. Find the population at the end of each decade. Describe the type of decline.Answer:
Question 4.The top eight runners finishing a race receive cash prizes. First place receives $200, second place receives $175, third place receives $150, and so on. Find the fifth through eighth place prizes. Describe the type of decline.Answer:
You May Like: Algebra 2 Unit Test Review Edgenuity
Lesson 81 Defining And Using Sequences And Series
Essential Question How can you write a rule for the nth term of a sequence?A sequence is an ordered list of numbers. There can be a limited number or an infinite number of terms of a sequence.a1, a2, a3, a4, . . . , an, . . .Terms of a sequenceHere is an example. 1, 4, 7, 10, . . . , 3n-2, . . .
EXPLORATION 1
Writing Rules for SequencesWork with a partner. Match each sequence with its graph. The horizontal axes represent n, the position of each term in the sequence. Then write a rule for the nth term of the sequence, and use the rule to find a10.a. 1, 2.5, 4, 5.5, 7, . . .b. 8, 6.5, 5, 3.5, 2, . . .c. \d. \e. \, 1, 2, 4, 8, . . .f. 8, 4, 2, 1, \, . . .
Communicate Your Answer
How can you write a rule for the nth term of a sequence?Answer:nth term of a sequencean = a1 + Question 3.What do you notice about the relationship between the terms in an arithmetic sequence and a geometric sequence? Justify yourAnswer:An arithmetic sequence has a constant difference between each consecutive pair of terms. This is similar to the linear functions that have the form y=mx +b. A geometric sequence has a constant ratio between each pair of consecutive terms.
Monitoring Progress
Write the first six terms of the sequence.Question 1.
Question 27.FINDING A PATTERNWhich rule gives the total number of squares in the nth figure of the pattern shown? Justify your answer.Answer:
In Exercises 3138, write the series using summation notation.Question 31.7 + 10 + 13 + 16 + 19Answer:
\Answer:
\Answer:
Recursive Formulas For Sequences
When discussing arithmetic sequences, you may have noticed that the difference between two consecutive terms in the sequence could be written in a general way:
a_n=a_+d
The above equation is an example of a recursive equation since the nth term can only be calculated by considering the previous term in the sequence. Compare this with the equation:
a_n=a_1+d.
In this equation, one can directly calculate the nth-term of the arithmetic sequence without knowing the previous terms. Depending on how the sequence is being used, either the recursive definition or the non-recursive one might be more useful.
A recursive geometric sequence follows the formula:
a_n=r\cdot a_
An applied example of a geometric sequence involves the spread of the flu virus. Suppose each infected person will infect two more people, such that the terms follow a geometric sequence.
The flu virus is a geometric sequence: Each person infects two more people with the flu virus, making the number of recently-infected people the nth term in a geometric sequence.
Using this equation, the recursive equation for this geometric sequence is:
a_n=2 \cdot a_
Recommended Reading: Word Problem Practice Algebra 1
Sequences And Series Chapter Test
Find the sum.\Answer:
\n2Answer:
\2k1Answer:
\4i1Answer:
Determine whether the graph represents an arithmetic sequence, geometric sequence, or neither. Explain your reasoning. Then write a rule for the nth term.Question 5.
2, 0, 3, 7, 12, . . .Answer:
Question 11.Write a recursive rule for the sequence 5, 20, 80, 320, 1280, . . .. Then write an explicit rule for the sequence using your recursive rule.Answer:
Question 12.The numbers a, b, and c are the first three terms of an arithmetic sequence. Is b half of the sum of a and c? Explain your reasoning.Answer:
Use the pattern of checkerboard quilts shown.a. What does n represent for each quilt? What does an represent?b. Make a table that shows n and an for n= 1, 2, 3, 4, 5, 6, 7, and 8.c. Use the rule an = \ to find an for n = 1, 2, 3, 4, 5, 6, 7, and 8.Compare these values to those in your table in part . What can you conclude? Explain.Answer:
Question 14.During a baseball season, a company pledges to donate $5000 to a charity plus $100 for each home run hit by the local team. Does this situation represent a sequence or a series? Explain your reasoning.Answer:
Lesson 82 Analyzing Arithmetic Sequences And Series
Essential Question How can you recognize an arithmetic sequence from its graph?In an arithmetic sequence, the difference of consecutive terms, called the common difference, is constant. For example, in the arithmetic sequence 1, 4, 7, 10, . . . , the common difference is 3.
EXPLORATION 1
Recognizing Graphs of Arithmetic SequencesWork with a partner. Determine whether each graph shows an arithmetic sequence. If it does, then write a rule for the nth term of the sequence, and use a spreadsheet to fond the sum of the first 20 terms. What do you notice about the graph of an arithmetic sequence?
EXPLORATION 2
Finding the Sum of an Arithmetic SequenceWork with a partner. A teacher of German mathematician Carl Friedrich Gauss asked him to find the sum of all the whole numbers from 1 through 100. To the astonishment of his teacher, Gauss came up with the answer after only a few moments. Here is what Gauss did:Explain Gausss thought process. Then write a formula for the sum Sn of the first n terms of an arithmetic sequence. Verify your formula by finding the sums of the first 20 terms of the arithmetic sequences in Exploration 1. Compare your answers to those you obtained using a spreadsheet.
Communicate Your Answer
How can you recognize an arithmetic sequence from its graph?Answer:
Find the sum of the terms of each arithmetic sequence.a. 1, 4, 7, 10, . . . , 301b. 1, 2, 3, 4, . . . , 1000c. 2, 4, 6, 8, . . . , 800Answer:
Which is different? Find both answers.Answer:
\Answer:
You May Like: Fsa Warm Ups Grade 5 Answer Key
Algebra 2 Sequences And Series Worksheet
Algebra 2 Sequences And Series Worksheet It is actually tedious whenever your children check with you in aiding these algebra house functions, and you are not able to do this home works, or you may not find out about them where you have not carried out algebra within your higher school days and nights. This sort of scenario is very stressful and with the help of some outstanding Algebra aiding tools as well as your youngsters are nicely-ready for coming up test. At this point, the net will help you to solve your issue you will find a variety of Algebra 2 Sequences And Series Worksheet and some other tools on the web, which will help the hard understanding procedure. Nonetheless, these algebra equipment are a great way to improve your math ability and a few practice will give more positive aspects in forthcoming math check. These worksheets include thousands of difficulties and equations where one can test oneself. And you could obtain an answer crucial for many these issues because website.
Sequences And Series Chapter Review

8.1 Defining and Using Sequences and Series
Question 1.Describe the pattern shown in the figure. Then write a rule for the nth layer of the figure, where n = 1 represents the top layer.Answer:
Write the series using summation notation.Question 2.
Question 12.Find the sum [la
You take a job with a starting salary of $37,000. Your employer offers you an annual raise of $1500 for the next 6 years. Write a rule for your salary in the nth year. What are your total earnings in 6 years?Answer:
8.3 Analyzing Geometric Sequences and Series
Question 14.Tell whether the sequence 7, 14, 28, 56, 112, . . . is geometric. Explain your reasoning.Answer:
Write a rule for the nth term of the geometric sequence. Then graph the first six terms of the sequence.Question 15.25, 10, 4, \ , . . .Answer:
Find the sum \5i1 .Answer:
8.4 Finding Sums of Infinite Geometric Series
Question 19.Consider the infinite geometric series 1, \ Find and graph the partial sums Sn for n= 1, 2, 3, 4, and 5. Then describe what happens to Sn as n increases.Answer:
Question 20.Find the sum of the infinite geometric series 2 + \, if it exists.Answer:
Write the repeating decimal 0.1212 . . . as a fraction in simplest form.Answer:
8.5 Using Recursive Rules with Sequences
Write the first six terms of the sequence.Question 22.a1 = 7, an = an-1 + 11Answer:
a1 = 26, an = \an-1.Answer:
Recommended Reading: How To Intimidate Someone Psychologically
Sequences And Series 81 83 Quiz
Describe the pattern, write the next term, and write a rule for the nth term of the sequence.Question 1.
\Answer:
\11k2Answer:
\4 )i+3Answer:
Question 18.Pieces of chalk are stacked in a pile. Part of the pile is shown. The bottom row has 15 pieces of chalk, and the top row has 6 pieces of chalk. Each row has one less piece of chalk than the row below it. How many pieces of chalk are in the pile?Answer:
Question 19.You accept a job as an environmental engineer that pays a salary of $45,000 in the first year. After the first year, your salary increases by 3.5% per year.a. Write a rule giving your salary an for your nth year of employment.b. What will your salary be during your fifth year of employment?c. You work 10 years for the company. What are your total earnings? Justify your answer.Answer: